Изгиб и растяжение или сжатие
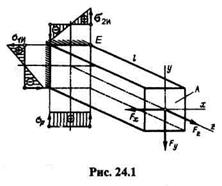
Рассмотрим брус длиной l постоянного поперечного сечения площадью А,защемленный одним концом и нагруженный на свободном конце произвольно направленной силой F,приложенной в центре тяжести сечения (рис. 24.1).
Разложим силу F на составляющие Fx, Fy и Fz.В результате действия этих составляющих получаем сочетание деформаций растяжения и поперечного изгиба в двух взаимно перпендикулярных плоскостях, причем касательными напряжениями изгиба будем в дальнейшем пренебрегать.
Применим принцип независимости действия сил и определим максимальные нормальные напряжения в опасном сечении (заделке):
|
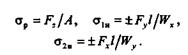
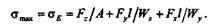
|
Максимальные суммарные напряжения возникнут в точке Е и будут напряжениями растяжения:
Эпюры нормальных напряжений растяжения и изгиба представлены на рис. 24.1.
Деформации растяжения и изгиба сочетаются, например, у крюков, винтов с отогнутой головкой, винтов слесарных тисков и т. д.
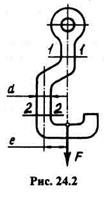
Пример 24.1. На рис. 24.2 показан стальной крюк, изготовленный из круглого прутка диаметром d = 24 мм. Эксцентриситет крюка е = 55 мм, сила тяжести поднимаемого груза F = 3 кН. Определить напряжения 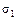 и
и 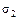 в сечениях 1—1 и 2—2 крюка.
в сечениях 1—1 и 2—2 крюка.
Решение. Применив метод сечений, видим, что в сечении 1—1 действует один силовой фактор — продольная сила N = F,а в сечении 2—2— два внутренних силовых фактора — продольная сила N = F иизгибающий момент Ми = F  е.
е.
Вычислим напряжения 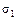 и
и 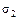 в сечениях 1— 1 и 2—2 .
в сечениях 1— 1 и 2—2 .
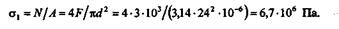
В сечении 2—2 имеем сочетание изгиба и растяжения. Вычислим максимальное суммарное напряжение
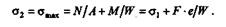
Учитывая, что е = 55 мм, a W 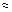 0,1d3, получим
0,1d3, получим
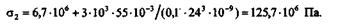
|
|
Внецентренное сжатие. Внецентренным сжатием называется такой вид деформации, когда сжимающая сила параллельна оси бруса, но точка ее приложения не совпадает с центром тяжести сечения (ранее изученную нами деформацию можно назвать центральным сжатием).
Рассмотрим брус прямоугольного сечения площадью А = bh (рис. 24.3, а),к которому на расстоянии е от оси приложена параллельная ей сила F.
В центре тяжести сечения вдоль оси приложим две противоположно направленные силы, равные по модулю силе F.Полученную систему трех сил
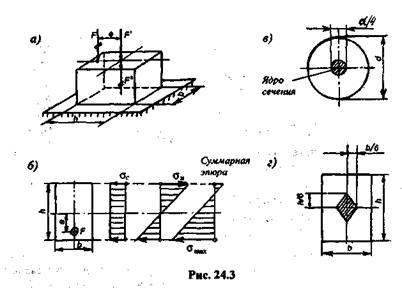
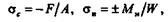
|
| а суммарные напряжения — по формуле |
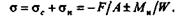
|
| Максимальные суммарные напряжения будут напряжениями сжатия: |
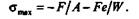
|
будем рассматривать как силу F,приложенную в центре тяжести, и пару сил с моментом т = Fe.Пользуясь принципом независимости действия сил, внецентренное сжатие будем рассматривать как сочетание центрального сжатия и чистого изгиба, причем соответствующие нормальные напряжения будем определять по формулам
Эпюры нормальных напряжений сжатия, изгиба и суммарная эпюра представлены на рис 24.3, б.
Чтобы в брусе не возникали напряжения растяжения (недопустимые, например, в кирпичной или в каменной кладке), должно выполняться неравенство
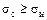 или F/A
или F/A 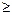 Fe/W , откуда е
Fe/W , откуда е 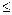 W/A.
W/A.
Для бруса прямоугольного сечения предельное значение эксцентриситета
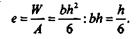
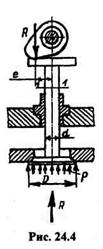
|
Для бруса круглого сечения диаметром d предельное значение эксцентриситета будет равно
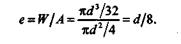
Ввиду полярной симметрии круга геометрическое место предельных положений точек приложения сжимающей силы F будет представлять собой окружность диаметром d/4.Круг, расположенный внутри этой окружности, называется ядром сечения (рис. 24.3, в).
Для прямоугольного бруса сечением b 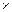 h ядро сечения представляет собой ромб с диагоналями h/3 и h/3(рис. 24.3, г).
h ядро сечения представляет собой ромб с диагоналями h/3 и h/3(рис. 24.3, г).
В случае внецентренного растяжения расчеты производятся по таким же формулам с учетом знаков напряжений.
Пример 24.2. На рис. 24.4 изображен клапанный механизм в момент открытия клапана. Определить максимальные напряжения в сечении 1-1 стержня тарелки клапана. Дано: давление на клапан р = 2МПа, диаметр клапана D = 40 мм, диаметр стержня тарелки d = 12 мм, максимальный эксцентриситет е=14мм.
Решение.Стержень тарелки клапанного механизма испытывает деформацию внецентренного сжатия, т. е. сочетания сжатия и изгиба. Максимальное напряжение сжатия вычисляется по формуле:
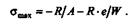
В нашем примере R — сила давления на дно тарелки клапанного механизма:
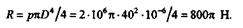
Площадь поперечного сечения стержня
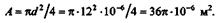
Момент сопротивления изгибу
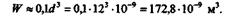
Подставляя числовые значения и произведя вычисления, находим
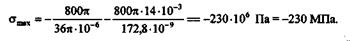
Гипотезы прочности
До сих пор мы рассматривали случаи сочетания основных деформаций, когда в поперечных сечениях бруса возникают только нормальные напряжения, которые в каждой точке можно было складывать алгебраически.
Часто встречаются и имеют большое практическое значение случаи сочетания основных деформаций, когда в поперечных сечениях возникают и нормальные и касательные напряжения, распределенные неравномерно и по разным законам. Для таких случаев опытное определение величин, характеризующих прочность, невозможно, поэтому при оценке прочности детали приходится основываться на механических характеристиках данного материала, полученных из диаграммы растяжения.
Как известно, при растяжении прочность пластичных материалов характеризуется пределом текучести, а хрупких — пределом прочности; эти напряжения считаются предельными, в зависимости от них вычисляют допускаемые напряжения.
Гипотезы прочности — это научные предположения об основной причине достижения материалом предельного напряженного состояния при сочетании основных деформаций.
Напряженные состояния при сочетании основных деформаций и при одноосном растяжении будем называть равноопасными или эквивалентными, если их главные напряжения отличаются от предельного для данного материала в одинаковое число раз, иначе говоря, коэффициенты запаса прочности для эквивалентных напряженных состояний одинаковы.
Эквивалентным напряжением называется такое условное напряжение при одноосном растяжении, которое равноопасно заданному случаю сочетания основных деформаций.
На основании гипотез прочности выводят формулы для вычисления эквивалентного напряжения, которое затем сопоставляют с допускаемым напряжением на растяжение. Таким образом, условие прочности при сочетании основных деформаций, когда в поперечных сечениях действуют и нормальные и касательные напряжения, будет иметь вид
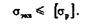
Сформулируем и охарактеризуем гипотезы прочности и приведем соответствующие формулы для вычисления эквивалентных напряжений.
Первая теория прочности, основанная на гипотезе наибольших нормальных напряжений, и в т 6 р а я теория прочности, основанная на гипотезе наибольших линейных деформаций, в настоящее время не применяются, и мы их рассматривать не будем.
Перейдем к рассмотрению теорий прочности, которыми пользуются в настоящее время.
1. Гипотеза наибольших касательных напряжений(третья теория прочности).
Согласно этой гипотезе, предложенной в конце XVIII в., опасное состояние материала наступает тогда, когда наибольшие касательные напряжения достигают предельной величины.
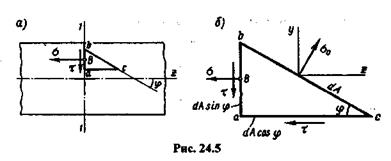
В § 20.5 мы установили, что при одноосном растяжении бруса максимальное касательное напряжение в наклонном сечении равно половине максимального нормального напряжения. Отсюда следует, что предельное касательное напряжение равно половине предельного нормального:
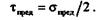
В том же параграфе мы установили, что в случае плоского напряженного состояния максимальное касательное напряжение равно полуразности главных напряжений:
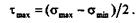
Чтобы вывести формулу для вычисления эквивалентных напряжений по третьей теории, рассмотрим брус, у которого в поперечном сечении действуют нормальные сги касательные 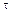 напряжения (рис. 24.5, а).
напряжения (рис. 24.5, а).
Внутри бруса вблизи некоторой точки В вырежем бесконечно малую призму abc, у которой грань аb совпадает с поперечным, грань ас — с продольным сечениями, а грань bс является главной площадкой, на которой действует главное напряжение 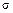 0.Согласно закону парности касательных напряжений, в грани ас призмы также будут действовать касательные напряжения
0.Согласно закону парности касательных напряжений, в грани ас призмы также будут действовать касательные напряжения 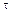 (рис. 24.5, б). Так как в продольном сечении бруса нормальных напряжений нет, то здесь мы имеем дело со случаем плоского напряженного состояния, который называют упрощенным.
(рис. 24.5, б). Так как в продольном сечении бруса нормальных напряжений нет, то здесь мы имеем дело со случаем плоского напряженного состояния, который называют упрощенным.
Рассмотрим равновесие призмы abc,для чего спроецируем все действующие на нее силы на оси z и y.Площадь грани bс обозначим dА:
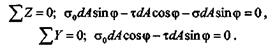
Разделив обе части равенств на dA, получим:
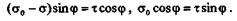
|
Оба равенства разделим на cos 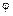 и, исключив из них tg
и, исключив из них tg 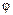 , получаем
, получаем
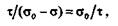
что дает квадратное уравнение
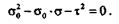
|
Решая это уравнение, получаем
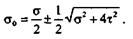
|
Таким образом, главные напряжения в наклонных площадках в зонах точки А бруса определяют по формулам
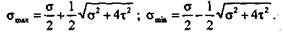
Следовательно, максимальные касательные напряжения будут (см. § 20.5):
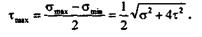
Поскольку 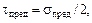 а эквивалентное напряжение не должно
а эквивалентное напряжение не должно
превышать предельного, то, применяя гипотезу наибольших касательных напряжений, имеем
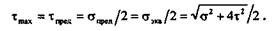
|
В результате получаем формулу для вычисления эквивалентных напряжений:
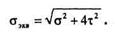
Гипотеза наибольших касательных напряжений хорошо подтверждается опытами, в особенности для пластичных материалов.
2. Гипотеза Мора(четвертая теория прочности).
К. О. Мор (1835—1918) — немецкий ученый в области сопротивления материалов и строительной механики, создатель одной из теорий прочности, графических методов определения напряжений при сложном напряженном состоянии (круг Мора) и т. д.
Гипотеза Мора предложена в начале XX в. Согласно этой гипотезе, опасное состояние материала наступает тогда, когда на некоторой площадке осуществляется наиболее неблагоприятная комбинация нормального и касательного напряжений.
Формула для вычисления эквивалентных напряжений имеет вид
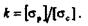
|
| где |
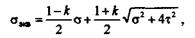
Эта формула одинаково пригодна как для хрупких, так и для пластичных материалов, при k = 1 она тождественна с формулой третьей теории прочности.
3. Энергетическая гипотеза (пятая, или энергетическая, теория прочности предложена в начале XX в.).
При деформации элементарной частицы тела в общем случае изменяются ее форма и ее объем. Таким образом, полная потенциальная энергия деформации состоит из двух частей: энергии формоизменения и энергии изменения объема. Энергетическая гипотеза прочности в качестве критерия перехода материала в предельное состояние принимает только энергию формоизменения.
Согласно этой гипотезе, опасное состояние материала в данной точке наступает тогда, когда удельная потенциальная энергия формоизменения для этой точки достигает предельной величины.
Формула для вычисления эквивалентных напряжений имеет вид
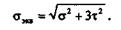
Эта формула для пластичных материалов хорошо подтверждается опытами и в настоящее время получила широкое распространение.
Отметим, что во всех приведенных выше формулах ст и т есть нормальные и касательные напряжения на площадке поперечного сечения, проходящего через опасную или предположительно опасную точку.
Изгиб и кручение
Сочетание деформаций изгиба и кручения испытывает большинство валов, которые обычно представляют собой прямые брусья круглого или кольцевого сечения.
При расчете валов мы будем учитывать только крутящий или изгибающий моменты, действующие в опасном поперечном сечении, и не будем принимать во внимание поперечные силы, так как соответствующие им касательные напряжения относительно невелики.
Максимальные нормальные и касательные напряжения у круглых валов вычисляют по формулам
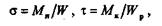
причем для круглых валов Wp = 2W.
При сочетании изгиба и кручения опасными будут точки опасного поперечного сечения вала, наиболее удаленные от нейтральной оси.
Применив третью теорию прочности, получим
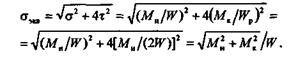
Выражение, стоящее в числителе, назовем эквивалентным моментом:
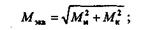
тогда расчетная формула для круглых валов принимает вид
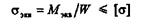
(валы обычно изготовляют из материала, у которого [ 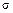 р ] = [
р ] = [ 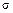 с] = [
с] = [ 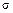 ] ).
] ).
По этой формуле расчет круглых валов ведут, как на изгиб, но не по изгибающему, а по эквивалентному моменту. Применив энергетическую теорию прочности, получим
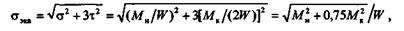
т. е. по энергетической теории прочности,
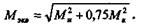
Для расчетов деталей на сочетание деформаций поперечного изгиба и кручения необходимо, как правило, составить расчетную схему конструкции и построить эпюры изгибающих и крутящих моментов, определить предположительно опасные сечения, после чего, применив одну из теорий прочности, произвести необходимые расчеты.
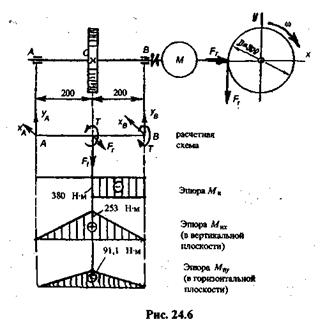
На рис. 24.6 в прямоугольных проекциях представлены: ведущий вал цилиндрической прямозубой передачи, расчетная схема вала и эпюры крутящего и изгибающих моментов в вертикальной и горизонтальной плоскостях. Эпюры построены на основании следующих данных:
передаваемая мощность Р = 40 кВт;
частота вращения вала п = 1000 об/мин;
диаметр делительной окружности зубчатого колеса D = 300 мм;
расстояние между опорами вала l = 400 мм;
радиальная нагрузка на зуб колеса Fr= 0,36 Ft, где Ft — окружная сила на колесе.
Проведем проверку прочности вала, изображенного на рис. 24.6, если дано:
|
диаметр вала в опасном сечении d=35 мм;
допускаемое напряжение для вала [ 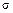 р] = 70 МПа.
р] = 70 МПа.
Прежде всего определим вращающий момент Т:
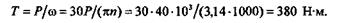
Далее определим окружную силу Ft:
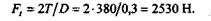
Определяем радиальную силу Fr:
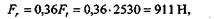
по этим данным строим эпюры Мк и Ми. Из эпюр видно, что опасное сечение расположено в месте закрепления зубчатого колеса.
Применим третью теорию прочности
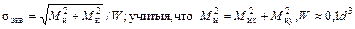
Взяв значения моментов из эпюр на рис.24.6, получим:
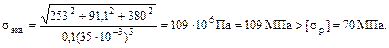
Следовательно, прочность вала недлостаточно.
275
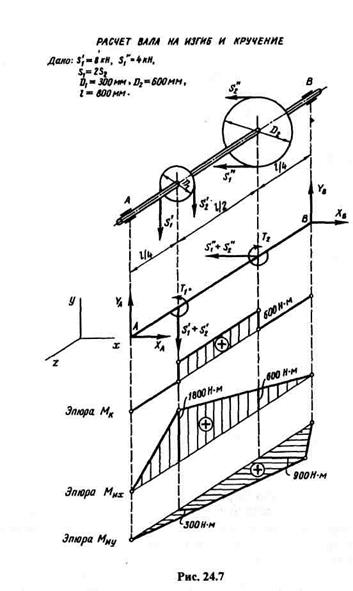
На рис. 24.7 в аксонометрической проекции представлены трансмиссионный вал ременной передачи, расчетная схема вала и эпюры крутящего и изгибающих моментов в вертикальной и горизонтальной плоскостях. Данные для расчетов приведены на рисунке.
Дата добавления: 2021-09-07; просмотров: 558;











