Вывод приближенной формулы для определения удельного заряда электрона
Удельным зарядом электрона называется отношение заряда электрона к его массе e/me.
Получим формулу для расчета зависимости анодного тока от напряжения для диода с плоскопараллельными электродами, рассматривая диод как конденсатор, емкость которого:
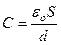
| (1) |
где eo — абсолютная диэлектрическая проницаемость вакуума, S и d— площадь пластин и расстояние между пластинами конденсатора соответственно.
Если катод нагрет до определенной температуры, то эмитированные им электроны устремляются к аноду, создавая ток:

| (2) |
(где q — заряд между катодом и анодом, t— время пролета электрона от катода к аноду), так как за время t все электроны, находящиеся между катодом и анодом, попадут на анод.
По определению, заряд, находящийся на обкладках плоского конденсатора, пропорционален напряжению на обкладках конденсатора U:
| q = C × U | (3) |
или

| (4) |
Тогда с учетом уравнения (4) уравнение (2) преобразуется:
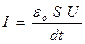
| (5) |
Умножив числитель и знаменатель (5) на d, получим:
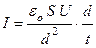
| (6) |
где d / t — средняя скорость движения электронов (Vср).
Если считать движение электронов равноускоренным и пренебречь их начальной скоростью, то можно записать:

| (7) |
где V — конечная скорость электрона, достигшего анода.
Из закона сохранения энергии найдем скорость V:
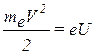 (8), (8), 
| (9) | |
где e – модуль заряда электрона, me – масса электрона.
Подставив в уравнение (6) значение конечной скорости из (9), с учетом условия (7) получим зависимость между током и напряжением:
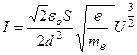
| (10) |
Точное выражение, с учетом изменения напряженности поля от катода к аноду, имеет вид:
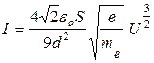
| (11) |
Эта формула носит название уравнения Богуславского — Ленгмюра (или закон трёх вторых).
Дата добавления: 2021-02-19; просмотров: 691;











