Взаимодействие света с границей раздела сред. Формулы Френеля

1. Поляризация света – это одно из фундаментальных свойств электромагнитного излучения. Оно состоит в неравноправности различных направлений в плоскости, перпендикулярной световому лучу. Поляризация присуща только поперечным волнам.

В электромагнитной теории света поперечность, а, следовательно, поляризованность световых волн вытекает с очевидностью. Но в эфирной волновой модели света, развивавшейся до конца XIX века, поперечность световых волн потребовала специальных доказательств. В таких явлениях, как интерференция и дифракция, вопрос о характере упругих колебаний не имеет принципиального значения. Оба эти явления реализуются как в случаях поперечных (свет), так и в случае продольных (звук) волн.

Термин «поляризация света» (от греческого polos – ось, полюс) предложил в 1808 г. Этьен Малюс.

Поперечность световых волн выражается в том, что колеблющиеся в них векторы напряженности электрического поля Е и индукции магнитного поля 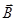перпендикулярны направлению распространения волны.

Естественный свет, излучаемый любым естественным источником, не поляризован. Хотя каждый элементарный цуг, излучаемый атомом, поляризован, плоскости поляризации разных цугов (плоскости колебаний Е) хаотично ориентированы в пространстве (рис.146 а и б).

Для того, чтобы получить пучок света, плоскости поляризации цугов в котором совпадают (рис.146-в) в оптике используются два способа: взаимодействие световых волн с границей раздела сред и взаимодействие света с анизотропной средой – кристаллом.

В настоящем параграфе будет рассмотрен первый способ, основанный на взаимодействии электромагнитной волны с границей раздела сред. Это взаимодействие зависит от того, как расположена относительно плоскости падения плоскость колебаний вектора Eволны. Выделим и рассмотрим здесь два случая:

а. Плоскость колебаний вектора E лежит в плоскости падения;

б. Плоскость колебаний вектора E лежит перпендикулярно плоскости падения.

2. Взаимодействие с границей раздела изотропных сред электромагнитной волны, вектор Е которой колеблется в плоскости падения. Напомним, что плоскость падения – это плоскость, в которой лежат падающий, отраженный, преломленный лучи и перпендикуляр, восстановленный в точку падения.

Пусть в точку О на границе раздела сред падает поляризованная электромагнитная волна, вектор Е которой колеблется в плоскости падения (рис.147). Обозначим амплитудные значения вектора напряженности электрического поля: падающей (E_a0), отраженной (E_a1) и преломленной (E_a2) волн. Полагаем, что свет не поглощается веществом сред. Как известно из курса электричества, касательная составляющая вектора напряженности электрического поля E на границе диэлектрических сред не испытывает разрыва, а нормальная составляющая терпит разрыв, подчиняющийся условию: e₁E_n1 = e₂E_n2. Здесь e₁ и e₂- диэлектрические проницаемости сред.

Отсюда можно получить два уравнения.

Для касательных составляющих: 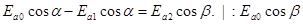. (17.1)

Сумма касательных составляющих векторов E_a0 и E_a1 в среде 1 равна касательной составляющей вектора E_a2 в среде 2.

Для нормальных составляющих: 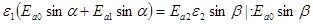. (17.2)

Разделим первое уравнение на 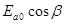, а второе на 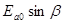. Коэффициенты отражения и пропускания электромагнитной волны по амплитуде обозначим соответственно 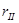и 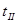: 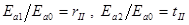. Получаем: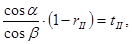 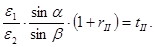(17.3, 17.4)

Так как 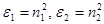, и 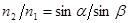, то коэффициент перед скобкой во втором уравнении принимает вид: 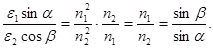(17.5)

Перепишем систему с преобразованным вторым уравнением и, разрешив ее относительно 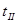и 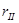, получим 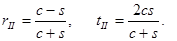(17.6)

Здесь 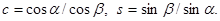(17.7)

Если использовать тригонометрические тождества, то формулы можно записать более компактно: 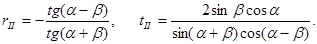(17.8)

В таком виде эти формулы получил впервые Огюст Френель в 1821 году. Он решил данную задачу в эфирной модели, в которой свет понимается как звуковая (механическая) волна в упругом эфире. Удивительно, что электромагнитная теория света сохранила вид формул (17.8), которые называют формулами Френеля.

3. Взаимодействие с границей раздела изотропных сред электромагнитной волны, векторEкоторой колеблется в плоскости, перпендикулярной плоскости падения. В этом случае на границе раздела сред вектор 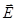имеетлишь одну составляющую, которая параллельна границе и противоположна оси OZ (рис.148). Составляющие вектора по осям OX и OY равны нулю. Для непрерывной касательной составляющей вектора 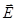имеем уравнение: 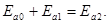(17.11)

Для нормальной составляющей вектора 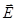уравнения нет. Поэтому воспользуемся магнитным полем волны. Вектор индукции 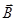в данном случае расположен точно так же, как вектор 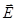в предыдущем случае. Поэтому условие непрерывности касательной составляющей вектора 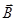записывается так же, как для вектора 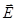в предыдущем случае (формула 17.1). B_a0cosa – B_a1cosa = B_a2cosb (17.12)

Перейдем в уравнении (17.12) от В к Е, используя связь между этими величинами. Так как B²½mm₀ = ee₀E², то 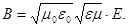(17.13)

Но 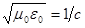- константа, 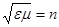- показатель преломления среды. Сократив все члены второго уравнения на с, получаем систему:

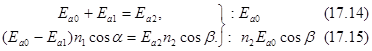Обозначив 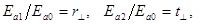получаем :

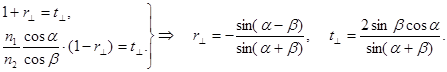(17.16)

Выражения для 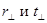так же совпали с результатами Френеля и тоже называются формулами Френеля.

4. Коэффициенты отражения и пропускания по интенсивности. Так как интенсивность света I пропорциональна квадрату амплитуды, 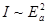, то коэффициенты по интенсивности равны квадрату соответствующего коэффициента по амплитуде.

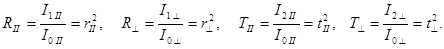(17.17)

Коэффициенты пропускания по интенсивност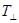и и 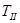выразим через коэффициенты отражения 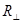и 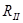, исходя из закона сохранения энергии 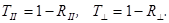(17.18)

При падении на границу раздела двух сред неполяризованного света его интенсив-ность I может быть представлена как сума интенсивностей двух его компонент, 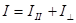. Здесь 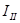- интенсивность компоненты, вектор 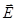которой колеблется в плоскости падения, 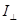- интенсивность компоненты, вектор 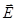которой перпендикулярен плоскости падения.

В силу случайной ориентации плоскостей колебании 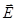отдельных цугов обе этих компоненты равноправны, 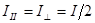. Отсюда можно найти суммарный коэффициент отражения по интенсивности неполяризованной волны, падающей на границу раздела сред. 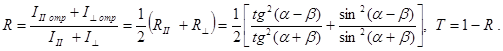(17.19), (17.20)

5. Закон Брюстера. Если a + b = 90°, то tg(a + b) = ∞, а 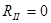. Следовательно, если луч естественного света падает на границу раздела сред под углом a = 90°– b, то в отражен-ном луче будут присутствовать только те волны, вектор 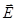которых перпендикулярен плоскости падения и отражаться будет полностью поляризованная волна. Угол полной поляризации из закона преломления. 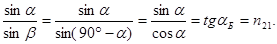(17.21)

Угол падения, при котором отраженный от диэлектрика свет полностью поляризован, открыл экспериментально в 1815 году Дэйвид Брюстер. Поэтому формулу 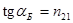называют законом Брюстера, а угол полной поляризации a_Б– углом Брюстера.

6. Поляризаторы– это устройства, позволяющие выделить из пучка естественного света поляризованную в одной плоскости компоненту.

R@0,45В качестве поляризатора может использоваться обычная стеклянная пластина, на которую свет падает под углом Брюстера (рис 149). Это так называемое зеркало Малюса. Недостаток зеркала Малюса – низкая интенсивность отраженного поляризованного пучка.

Для увеличения светосилы поляризатора А. Столетов предложил использовать в качестве зеркала Малюса не черное, а прозрачное стекло, складывая несколько пластинок в стопу (рис 150). Поскольку толщина пластинок много больше длины когерентности естественного света, то отраженные от пластинок лучи не интерферируют, а их интенсивности просто складываются. За счет этого коэффициент отражения стопы Столетова приближается к 50%.

7. Закон Малюса. Чтобы убедится в том, что свет поляризован, нужно на его пути поставить второй поляризатор, называемый в этом качестве анализатором (рис.151).

В 1810 году Этьен Малюс нашел закон изменения интенсивности линейно поляризованного света после его прохождения через анализатор. I = I₀cos²j. (17.22)

Здесь I₀ - интенсивность линейно поляризованного света, падающего на анализатор, j – угол между плоскостью поляризации света, падающего на анализатор, и плоскостью пропускания анализатора.

Закон Малюса вытекает из того, что через анализатор проходит составляющая вектора E₀ падающей волны, приходящейся на плоскость пропускания анализатора АА (рис.152). Очевидно, E = E₀cosj. Но интенсивность света пропорциональна квадрату амплитуды вектора E. Следовательно: I₀ = kE₀², I = kE² = kE₀²cos²j = I₀cos²j. Здесь k – коэффициент пропорциональности.

8. Отражение нормально падающих на поверхность лучей. При проектировании оптических приборов важно знать коэффициент отражения падающих нормально границе раздела сред лучей. Подстановка a = b = 0приводит в формулах Френеля к неопределенности 0/0. Поэтому преобразуем формулу для R (17.20) к малым углам a и b, близким к нулю.

При малых a и 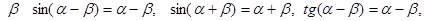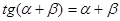. Отсюда: 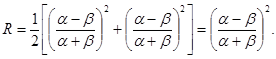(17.23)

Т.к. 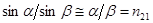, b = açn₁₂, 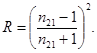(17.24)

Кривая зависимости коэффициента отражения света R от границы раздела сред симметрична относительно ординаты, соответствующей n₂çn₁ = 1 (рис.153). Это значит, что коэффициент отражения не зависит от того, с какой стороны падает на границу свет.

Чем больше отношение n₂çn₁, то есть чем сильнее отличаются среды, тем больше коэффициент отражения R. С ростом показателя преломления диэлектрика коэффициент отражения лучей от их поверхности, граничащей с воздухом, растет. От стекла с n = 1,5 отражается 4 % энергии падающих лучей, а от алмаза с n = 2,4 отражается 17 %. Сквозь двухлинзовый объектив, изготовленный из тяжелого флинта с n = 1,75, проходит всего лишь 70 % падающего света. Отсюда становится понятно, как велико положительное значение просветляющих покрытий.

С увеличением угла падения лучей a коэффициент отражения 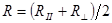монотонно растет от минимального значения, соответствующего нормальному падению лучей (формула 17.24) до 1 при a = 90° (рис.154). Поэтому зеркальные отражения низких берегов в спокойных водоемах почти так же ярки, как сами берега. Отражение в воде заходящего солнца так же почти не уступает по яркости самому солнцу.

На рисунке 154 слева показаны теоретические кривые для коэффициентов отражения видимого света от стекла (n = 1,5), а справа – от воды ( 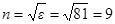). Внизу на графиках указанны углы a падения луча в градусах.