Биномиальное распределение и асимптотические формулы
Пример 1. По мишени производят четыре независимых выстрела. Вероятность попасть в мишень при каждом выстреле равна 0,8.
Для СВ X – числа возможных попаданий в мишень, составить ряд распределения и найти M(X), D(X), s(X).
Решение. Четыре независимых выстрела по мишени можно рассматривать как последовательность из четырех независимых испытаний, в каждом из которых событие А (попадание в мишень при одном выстреле) может появиться с вероятностью 0,8.
Поэтому СВ X имеет биномиальное распределение с параметрами
p = 0,8 и n = 4. Используя формулу (1.33) 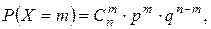 где
где
q = 1 – p, получим
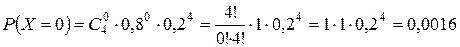
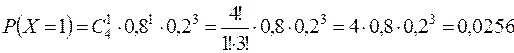
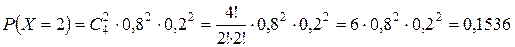
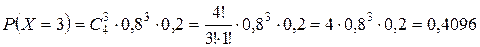
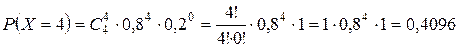
Поверка: å pi = 1.
| X | |||||
| P | 0,0016 | 0,0256 | 0,1536 | 0,4096 | 0,4096 |
Найдем числовые характеристики СВ X, распределенной по биномиальному закону.
M(X) = n × p = 4 × 0,8 = 3,2
D(X) = n × p × q = 4 × 0,8 × 0,2 = 0,64
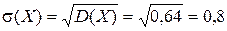
Пример 2. Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течение времени Т равна 0,001. Найти вероятность того, что за время Т откажут ровно два элемента.
Пусть СВ X – число элементов, которые могут отказать за время Т. Так как p мало, а n достаточно велико, то искомую вероятность вычислим приближенно по формуле Пуассона (1.41)
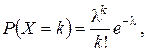 где l = n × p = 1000 × 0,001 = 1.
где l = n × p = 1000 × 0,001 = 1.
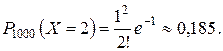
Пример 3. Вероятность выхода из строя изделия за время испытания на надежность p = 0,05. Какова вероятность того, что за время испытаний 100 изделий выйдут из строя:
1) не менее 4 изделий,
2) ровно 5 изделий.
1) По условию n = 100, p = 0,05, q = 1 – p = 0,95.
Решение. Воспользуемся интегральной теоремой Муавра-Лапласа
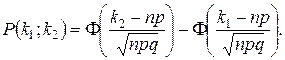
Значения функции Лапласа 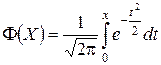 возьмем из таблицы 2.
возьмем из таблицы 2.
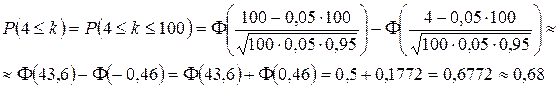
2) Воспользуемся локальной теоремой Лапласа (1.35)
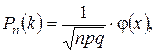 где
где 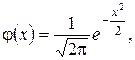
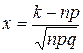
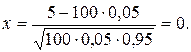 Из таблицы находим значение функции
Из таблицы находим значение функции
j(0) = 0,3989.
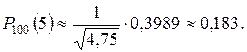
Дата добавления: 2021-12-14; просмотров: 682;











