Потенциальная энергия. Закон сохранения энергии в механике. Сила и потенциальная энергия.

Для консервативных сил, работа которых не зависит от формы пути, можно ввести важное понятие потенциальной энергии.Давайте какое-либо произвольное положение системы, характеризуемое заданием координат ее материальных точек, условно примем за нулевое. Тогда

работа, совершаемая консервативными силами при переходе системы из некоторого положения в нулевое, называется потенциальной энергией U системы в этом положении.

Работа консервативных сил не зависит от пути перехода, а поэтому потенциальная энергия системы при фиксированном нулевом положении зависит только от координат материальных точек системы в рассматриваемом положении. Иными словами,

потенциальная энергия системы U является функцией только ее координат.

Значение потенциальной энергии, вообще говоря, зависит от того, какое положение системы условно принято за нулевое. Если за нулевое принять положение 0, то в положении 1 система будет обладать потенциальной энергией U= A₁₀, равной работе консервативных сил при переходе системы из положения 1 в положение 0. Если же за нулевое принять положение 0', то потенциальная энергия будет равна (U' = А_10’. Вследствие консервативности сил

А_10’= А₁₀ + А_оо, или U₁^’ = U₁ + А_оо’. (7.1)

Работа A_00' постоянна, то есть не зависит от координат системы в рассматриваемом состоянии 1. Она полностью определяется выбором нулевых положений 0 и 0’.

Мы видим, таким образом, что при замене одного нулевого положения другим потенциальная энергия системы изменяется на постоянную величину. Неопределенность можно усилить еще больше, если условиться считать потенциальную энергию в нулевом положении равной не нулю, а какому-либо постоянному произвольному значению. Тогда в приведенном выше определении вместо потенциальной энергии следует говорить об ее разностив двух положениях.

Разностью потенциальных энергий в рассматриваемом и нулевом положениях называется работа, совершаемая консервативными силами при переходе системы из рассматриваемого положения в нулевое.

Таким образом, потенциальная энергия определена не однозначно, а с точностью до произвольной постоянной.

Пусть система перешла из положения 1 в положение 2 по какому-либо пути 12. Тогда, как следует из рис. 7.2,

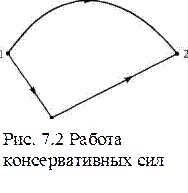А₁₂ = А₁₀ + А₀₂ = А₁₀ - А₂₀ = U₁ - U₂ = -U₂ – U₁ ,

то есть работа консервативных сил равна убыли потенциальной энергии системы при переходе ее из точки 1 в точку 2.

С другой стороны, работа силы равна приращению кинетической энергии системы

A_l2 = U_l-U₂ = K₂-K₁, (7.2)

поэтому

K₁+ U₁= K₂ + U₂. (7.3)

Сумма кинетической и потенциальной энергии системы называется ее полной энергиейЕ. Мы получили, что полные энергии в положениях 1 и 2 равны: Е₁ = Е₂, или, что то же самое, полная энергия сохраняется:

Е= К + U = const. (7.4)

Таким образом,

В системе с одними только консервативными (и гироскопическими) силами полная энергия остается неизменной. Могут происходить лишь превращения потенциальной энергии в кинетическую и обратно, но полный запас энергии системы измениться не может.

Это положение называется законом сохранения энергиив механике. Примеры потенциальной энергии в некоторых простейших случаях:

-U= mgh — потенциальная энергии однородного поля тяжести. Начало отсчета h = 0.

-U= kx²/2 — потенциальная энергия растянутой пружины. Начало отсчета х= 0.

-U= -GMm/r — потенциальная энергия гравитационного притяжения двух точечных масс т и M. За начало отсчета выбрана бесконечно удаленная точка.