Изотропия пространства. Закон сохранения момента импульса. Движение в центральном поле

Итак, мы пришли к выводу, что законы сохранения импульса и энергии связаны со свойствами однородности пространства времени. Третий важный закон сохранения получается, если пространство изотpопно,то есть если повороты на произвольный угол вокруг произвольной оси не изменяют потенциальную энергию системы.

Рассмотрим замкнутую систему, состоящую из N материальных точек. Потенциальная энергия этой системы является функцией координат материальных точек:

U = U(r₁,r₂,...,r_N). (8.1)

Произведем теперь бесконечно малый поворот системы и потребуем, чтобы ее потенциальная энергия оставалась при этом неизменной. Для этого введем вектор бесконечно малого поворота δφ, величина которого равна углу δφповорота, а направление совпадает с осью поворота (причем так, что направление поворота отвечает правилу винта по отношению к направлению δφ).

При таком повороте каждая материальная точка системы, характеризуемая радиус-вектором r_a, сместится на величину:

δr_a = [δφ × r_a]. (8.2)

В результате потенциальная энергия получит приращение

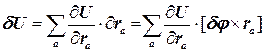(8.3)

Но в соответствии со вторым законом Hьютона производная ∂U/∂r_a равна р . Следовательно,

δU =- 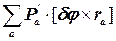(8.4)

Произведем в этом равенстве циклическую перестановку векторов, при которой векторное произведение не изменяется:

А[B × C] = C [A × B] = B [C × A]. (8.5)

В результате этой перестановки, вынося δφ за знак суммы, имеем

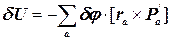(8.6)

Это изменение потенциальной энергии должно быть равно нулю при любом δφ в силу изотропии пространства. Следовательно,

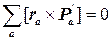(8.7)

Прибавим к этому равенству очевидное соотношение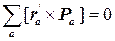

В результате

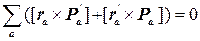. (8.8)

Выражение, стоящее в круглых скобках, представляет собой полную производную по времени от векторного произведения [r_a × p_a]:

Следовательно,

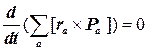(8.9)

Поэтому для замкнутой системы величина

L = 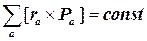(8.10)

остается постоянной в процессе движения. Она называется моментом импульсасистемы и представляет собой аксиальный вектор. Как следует из его определения, момент импульса — величина аддитивная, что означает, что момент импульса системы равен сумме моментов импульсов составляющих ее материальных точек. Так же как и в случае импульса, аддитивность этой величины не зависит от наличия или отсутствия взаимодействия между частицами.

Ранее мы ввели понятие момента импульса через момент инерции (формула (5.4) 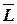= 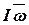). Эти выражения идентичны, первое связывает момент импульса с импульсом тела, а второе – выражает момент импульса через величины вращательного движения.

Для замкнутой системы материальных тел момент импульса остается величиной постоянной, т.е. L = const.

В результате у замкнутой системы при движении сохраняются следующие величины: энергия, импульс и момент импульса.

Поскольку в определение момента импульса входят pадиус­вектоpы частиц, то его значение, вообще говоря, зависит от выбора начала координат. Радиус­вектоpы r иr' одной и той же точки по отношению к началам, отстоящим на вектор b, связаны соотношением
r_a = r’ + b. Поэтому имеем

L= L'+[b 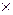P], (8.11)

где P =åp_a — суммарный импульс системы. Из этой формулы видно, что только в том случае, когда система как целое покоится (то есть когда P = 0), ее момент импульса не зависит от выбора начала координат. На законе сохранения момента импульса эта неопределенность его значения, разумеется, не сказывается, так как у замкнутой системы импульс тоже сохраняется.

Хотя закон сохранения всех трех компонент момента импульса (относительно произвольного начала координат) справедлив только для замкнутой системы, в более ограниченном виде этот закон может распространяться и на системы, находящиеся во внешнем силовом поле (гравитационном, электромагнитном). Из приведенного выше вывода видно, что всегда сохраняется проекция момента на такую ось, относительно которой данное поле симметрично, и поэтому механические свойства системы не изменяются при любом повороте вокруг этой оси; при этом, конечно, момент должен быть определен относительно какой-нибудь точки (начала координат), лежащей на этой оси.

Наиболее важным случаем такого рода является поле с центральной симметрией,то есть поле, в котором потенциальная энергия зависит только от расстояния до некоторой определенной точки (центра) в пространстве. Очевидно, что при движении в таком поле сохраняется проекция момента на любую ось, проходящую через центр. Другими словами, сохраняется вектор M момента, определенного не относительно произвольной точки пространства, а относительно центра поля (пример — движение планеты в поле силы тяжести Солнца).

Если имеется однородное поле вдоль оси z, то и здесь сохраняется величина L_z, но начало координат уже может быть выбрано произвольным образом. В конкретной задаче это может быть, например, однородное магнитное или электрическое поле.