I.2.4 ВТОРОЙ ЗАКОН (ВТОРОЕ НАЧАЛО) ТЕРМОДИНАМИКИ
Вторым законом (началом) термодинамики называется полученное опытным путём утверждение о невозможности построения вечного двигателя второго рода. Второй закон имеет две наиболее распространённые формулировки, которые эквивалентны друг другу:
1. невозможен процесс, единственным результатом которого является превращение всей теплоты, полученной от некоторого тела, в эквивалентную ей работу;
2. невозможен процесс, единственным результатом которого является передача энергии в форме теплоты от тела менее нагретого к телу более нагретому.
Прежде чем переходить к рассмотрению второго начала термодинамики введём следующие основные понятия: «равновесное состояние», «равновесный процесс», «замкнутые и незамкнутые, обратимые и необратимые процессы».
Равновесным состоянием системы называется такое состояние, при котором все параметры системы имеют определенные одинаковые для всех точек системы значения, остающиеся при неизменных внешних условиях постоянными сколь угодно долго.
Процесс, состоящий из непрерывной последовательности равновесных состояний, называется равновеснымили квазистатическим.
Все термодинамические процессы, протекающие в замкнутой системе, можно подразделить на обратимые и необратимые.
Термодинамический процесс обратим, если, протекая в обратном направлении, он возвращает систему в исходное состояние без затрат энергии, проходя ту же последовательность промежуточных состояний. В противном случае термодинамические процессы называются необратимыми. Они протекают самопроизвольно только в одном направлении.
Примеры обратимых процессов: движение планет, незатухающие колебания маятника, упругий удар, цикл Карно.
Примеры необратимых процессов: затухающие колебания маятника, неупругий удар, процессы с трением, диффузия, теплопередача, теплообмен.
Большинство процессов в технике представляют собой необратимые процессы или, по крайней мере, содержат этапы, являющиеся необратимыми процессами.
Совокупность процессов, в результате которых система возвращается в исходное состояние, называется круговым процессом (циклом). На диаграмме процессов цикл изображается замкнутой кривой (рис.10)
а) б)
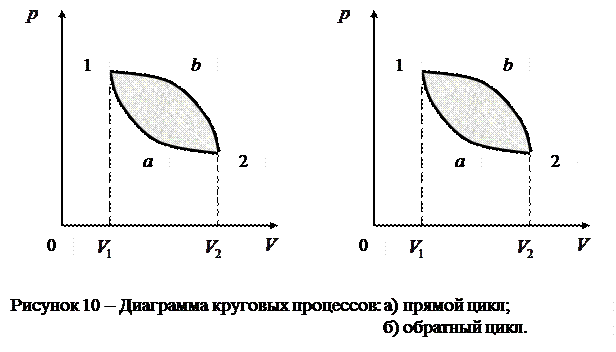 |
Цикл, совершаемый идеальным газом, можно разбить на процессы расширения (1-2) и сжатия (2-1) газа. Работа расширения (определяется площадью фигуры 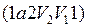 положительна
положительна 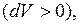 работа сжатия (определяется площадью фигуры
работа сжатия (определяется площадью фигуры 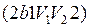 ) отрицательна
) отрицательна 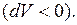 Следовательно, работа, совершаемая газом за цикл, определяется площадью, охватываемой замкнутой кривой. Если за цикл совершается положительная работа
Следовательно, работа, совершаемая газом за цикл, определяется площадью, охватываемой замкнутой кривой. Если за цикл совершается положительная работа 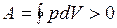 (цикл протекает по часовой стрелке), то он называется прямым (рис. 10, а), если за цикл совершается отрицательная работа
(цикл протекает по часовой стрелке), то он называется прямым (рис. 10, а), если за цикл совершается отрицательная работа 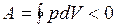 (цикл протекает против часовой стрелки), то он называется обратным (рис. 10, б).
(цикл протекает против часовой стрелки), то он называется обратным (рис. 10, б).
В основе работы всех циклических тепловых машин лежат круговые процессы.
Примером круговых процессов является цикл Карно.
Циклом Карно называется прямой обратимый круговой процесс (рис.11), состоящий из двух изотерм (1 - 1/) и (2 - 2/) и двух адиабат (1 - 2) и (1/ - 2/).
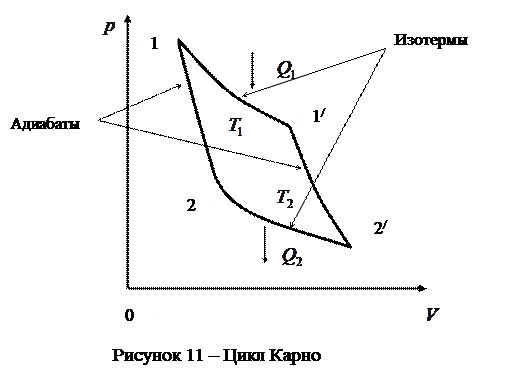
При изотермическом расширении (1 - 1/) рабочее тело получает от нагревателя – источника энергии с постоянной температурой Т1 – количество теплоты 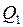 . При изотермическом сжатии (2 - 2/) рабочее тело отдаёт холодильнику, имеющему постоянную температуру
. При изотермическом сжатии (2 - 2/) рабочее тело отдаёт холодильнику, имеющему постоянную температуру 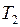
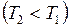 , количество теплоты
, количество теплоты 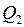 . При адиабатном расширении и сжатии энергия извне к рабочему телу не поступает, и эти процессы происходят за счёт изменения его внутренней энергии.
. При адиабатном расширении и сжатии энергия извне к рабочему телу не поступает, и эти процессы происходят за счёт изменения его внутренней энергии.
Прежде, чем дать формулировку теоремы Карно, необходимо ввести понятие термического коэффициента полезного действия (к.п.д.).
Термическим (термодинамическим) коэффициентом полезного действия ( 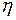 ) произвольного цикла называется отношение работы
) произвольного цикла называется отношение работы 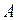 , совершенной рабочим телом в прямом цикле, к количеству теплоты
, совершенной рабочим телом в прямом цикле, к количеству теплоты 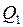 , сообщенному рабочему телу нагревателем
, сообщенному рабочему телу нагревателем
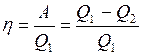 . (I.67)
. (I.67)
Теорема Карно: термический коэффициент полезного действия обратимого цикла Карно не зависит от состава рабочего тела и всегда выражается формулой:
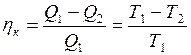 , (I.68)
, (I.68)
где 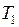 – температура нагревателя;
– температура нагревателя; 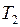 – температура холодильника.
– температура холодильника.
· Из всех циклических процессов цикл Карно обладает наибольшим КПД. Большее значение КПД, хотя и не противоречит первому закону, но невозможно в силу ограничений, накладываемых вторым законом термодинамики.
· КПД цикла Карно не зависит от природы рабочего тела и является функцией только температуры холодильника и нагревателя.
· Максимальное значение КПД (идеальный случай) любых тепловых двигателей всегда меньше единицы и определяется по выше приведенной формуле. В действительности КПД всегда меньше этого значения вследствие потерь и прочих причин. Таким образом, данная формула определяет верхний предел КПД 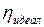 .
.
Важным в этом параграфе является и понятие энтропии.
Функцию состояния, дифференциалом которой является, 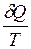 и называют энтропией, которая обозначается
и называют энтропией, которая обозначается 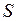 .
.
В основе термодинамических применений энтропии лежит следующее соотношение
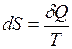 , (I.69)
, (I.69)
где 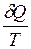 - приведённое количество теплоты, сообщаемое телу на бесконечно малом участке процесса.
- приведённое количество теплоты, сообщаемое телу на бесконечно малом участке процесса.
При обратимом процессе изменение энтропии 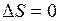 . При необратимом процессе изменение энтропии
. При необратимом процессе изменение энтропии 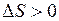 .
.
Энтропия играет важную роль в различных термодинамических процессах.
Таблица – 2 Изменение энтропии при любых термодинамических процессах
| Изменение энтропии | Процесс |
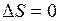
| Обратимый, может протекать как в прямом, так и в обратном направлениях |
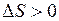
| Необратимый, самопроизвольно протекает только в одном направлении |
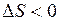
| Не может протекать самопроизвольно, необходим подвод энергии извне |
Все процессы в природе протекают в направлении увеличения энтропии.
Использование понятия энтропии позволяет очень просто сформулировать второй закон термодинамики: энтропия замкнутой системы не может уменьшаться
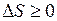 . (I.70)
. (I.70)
Больцман установил связь энтропии с вероятностью термодинамического состояния 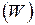
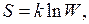 (I.71)
(I.71)
где 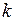 – постоянная Больцмана, W – вероятность, равная числу микросостояний термодинамической системы, соответствующих данному макроскопическому состоянию.
– постоянная Больцмана, W – вероятность, равная числу микросостояний термодинамической системы, соответствующих данному макроскопическому состоянию.
Энтропия характеризует вероятность, с которой устанавливается то или иное состояние. Кроме того, энтропия является мерой хаотичности или необратимости.
Теорема Нернста (третье начало термодинамики): энтропия любого тела стремится к нулю при стремлении к нулю температуры
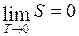 . (I.72)
. (I.72)
Дата добавления: 2016-09-06; просмотров: 3942;











