Сила и потенциальная энергия
Зная силу как функцию координат материальной точки F(x,y,z), можно путем интегрирования (нахождения работы) определить потенциальную энергию системы
U1=U(x,y,z)-U(0)=A10=-A01=- 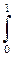 Fdr (7.5)
Fdr (7.5)
(знак минус перед интегралом обусловлен тем, что при интегрировании в этой формуле мы движемся от точки 0 к точке 1).
Другая задача — вычисление силы F(x,y,z) по заданной потенциальной энергии U(x,y,z). Это, естественно, обратная операция — дифференцирование. Пусть у нас есть две бесконечно близкие точки, r+ dг и г. Тогда
U(r+dr) – U(r) =dU= -F • dr. (7.6)
Расписывая скалярное произведение, получаем
dU = -(Fx dx + Fy dy + Fz dz). (7.7)
Следовательно, 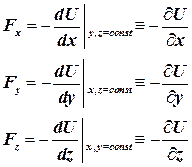 (7.8)
(7.8)
(это есть частная производная)
Таким образом, компоненты силы можно найти, дифференцируя потенциальную энергию системы по координатам х,у и z.
Если ввести единичные орты i, j и kвдоль осей координат X, Y и Z, то формулу для силы можно будет записать следующим образом:
F = Fxi+Fyj+Fzk=-( 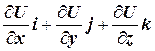 )= -gradU. (7.9)
)= -gradU. (7.9)
где мы ввели обозначения:
grad U= 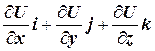 (7.10)
(7.10)
Величина, стоящая слева, называется градиентом скалярной функцииU (U(x,y,z) — скаляр). Эта величина является вектором, поскольку определяет действующую на материальную точку силу. Таким образом, дифференцирование по координатам скалярной функции дает вектор.
Наряду с обозначением градиента как gradU применяется обозначение ÑU, где оператор Ñ (набла) определяется следующим образом:
Ñ= 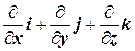
Используя это обозначение, мы можем записать
gradU = Ñ U = ( 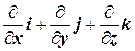 ) U=
) U= 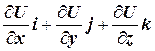 (7.11)
(7.11)
Дата добавления: 2017-09-01; просмотров: 948;











