Движение в центральном поле

Рассмотрим задачу об относительном движении двух взаимодействующих частиц, которая допускает полное решение в общем виде, — задачу двух тел.Потенциальная энергия взаимодействия двух частиц зависит лишь от расстояния между ними, то есть от абсолютной величины разности их pадиус­вектоpов. Энергия такой системы может быть представлена в виде

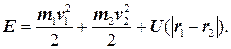(8.12)

Введем вектор взаимного расстояния обеих точек

r = r₁ − r₂ (8.13)

и поместим начало координат в центр инерции, что дает

m₁r₁+m₂r₂ = 0. (8.14)

Из двух последних равенств находим

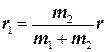и

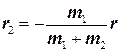
Дифференцируя эти выражения по времени, получаем

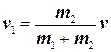и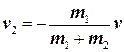

где v = dr/dt — относительная скорость движения двух материальных точек. Кинетическая энергия равна

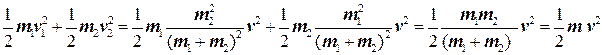
где мы ввели обозначение

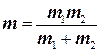(8.15)

Величина m называется приведенной массой.В результате в системе центра инерции полная энергия равна

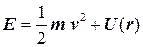(8.16)

Таким образом, задача двух тел свелась к движению одной материальной точки с приведенной массой в центральном полеU(r). Центральным называется поле, потенциальная энергия которого зависит лишь от расстояния до определенной неподвижной точки.

Как мы уже говорили, при движении в центральном поле сохраняется момент импульса относительно центра поля. Для одной частицы

L=[r×p]. (8.17)

Поскольку векторы Lиr взаимно перпендикулярны, постоянство момента (в данном случае по направлению) означает, что при движении частицы ее радиус-вектор r все время остается в одной плоскости, перпендикулярной к вектору L.