I.1.4 ИДЕАЛЬНЫЙ ГАЗ. ГАЗОВЫЕ ЗАКОНЫ. УРАВНЕНИЕ СОСТОЯНИЯ ИДЕАЛЬНОГО ГАЗА
В молекулярно – кинетической теории рассматривается идеализированная модель реальных газов – идеальный газ.
Идеальный газ – газ, молекулы которого не взаимодействуют друг с другом на расстоянии и имеют исчезающе малые собственные размеры. У реальных газов молекулы испытывают силы межмолекулярного взаимодействия.
При взаимных столкновениях и соударениях со стенками сосуда молекулы идеального газа ведут себя как абсолютно упругие шары с диаметром 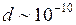 м (эффективный диаметр молекулы), зависящим от химической природы газа. Наличие эффективного диаметра означает, что между молекулами действуют силы взаимного отталкивания. Межмолекулярные силы притяжения быстро убывают с увеличением расстояния
м (эффективный диаметр молекулы), зависящим от химической природы газа. Наличие эффективного диаметра означает, что между молекулами действуют силы взаимного отталкивания. Межмолекулярные силы притяжения быстро убывают с увеличением расстояния 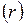 между молекулами и не проявляются практически при
между молекулами и не проявляются практически при 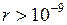 м.
м.
Существующие в действительности газы при не слишком низких температурах и достаточно малых давлениях – разреженные газы – по своим свойствам близки к идеальному газу. Например, гелий при комнатной температуре и атмосферном давлении с хорошим приближением подчиняется законам идеальных газов.
Опытным путем был установлен целый ряд законов, описывающих поведение идеальных газов.
Закон Бойля-Мариотта: для данной массы газа при постоянной температуре произведение давления газа на его объем есть величина постоянная
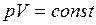 . (I.3)
. (I.3)
При 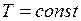 ;
; 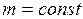 .
.
Для 2-х состояний
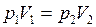 . (I.4)
. (I.4)
Изотерма – кривая, изображающая зависимость между величинами 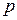 и
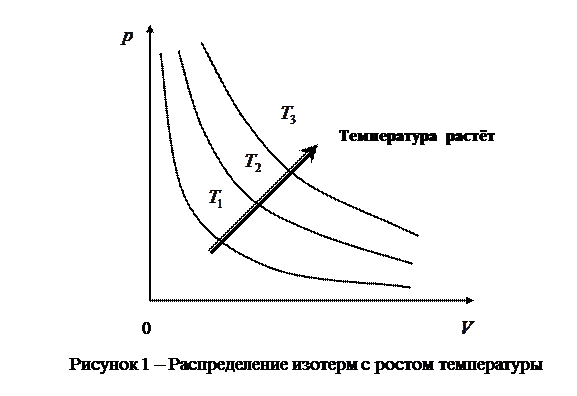
и 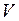 , характеризующими свойства вещества при постоянной температуре. Изотермы представляют собой равнобочные гиперболы, расположенные на графике тем выше, чем выше температура, при которой происходит процесс (рис.1).
, характеризующими свойства вещества при постоянной температуре. Изотермы представляют собой равнобочные гиперболы, расположенные на графике тем выше, чем выше температура, при которой происходит процесс (рис.1).
Закон Гей-Люссака: объем данной массы газа при постоянном давлении изменяется линейно с температурой
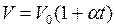 . (I.5)
. (I.5)
При 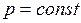 ;
; 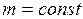
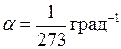 (в СИ:
(в СИ: 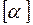 = K–1).
= K–1).
Или другая форма записи закона
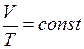 . (I.6)
. (I.6)
Для 2-х состояний
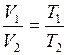 . (I.7)
. (I.7)
.
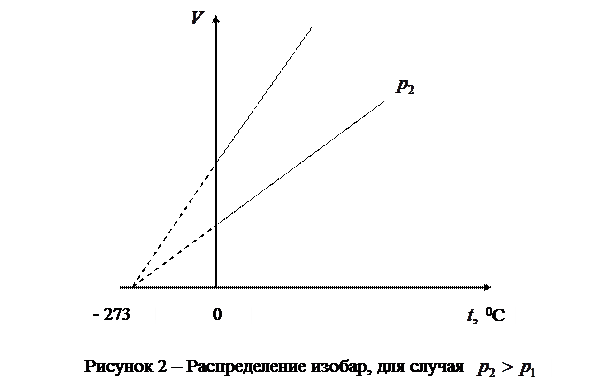
На диаграмме в координатах 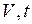 (рис.2) этот процесс изображается прямой, называемой изобарой.
(рис.2) этот процесс изображается прямой, называемой изобарой.
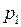
Закон Шарля: давление данной массы газа при постоянном объеме изменяется линейно с температурой
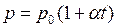 .(I.8)
.(I.8)
При 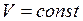 ;
; 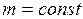
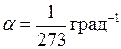 (в СИ:
(в СИ: 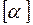 = K–1).
= K–1).
Или другая форма записи закона
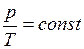 . (I.9)
. (I.9)
Для двух состояний
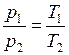 . (I.10)
. (I.10)
На диаграмме в координатах 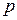 ,
, 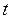 (рис.3) этот процесс изображается прямой, называемой изохорой.
(рис.3) этот процесс изображается прямой, называемой изохорой.
|
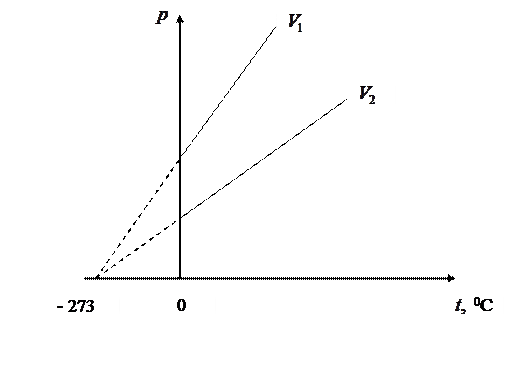
Из формул (I.4) и (I.8) следует, что изобары и изохоры пересекают ось температур в точке 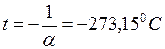 , определяемой из условия
, определяемой из условия 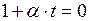 . Если сместить начало отсчёта в эту точку, то происходит переход к шкале Кельвина
. Если сместить начало отсчёта в эту точку, то происходит переход к шкале Кельвина 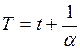 .
.
Французский физик и инженер Б. Клапейрон вывел уравнение состояния идеального газа, объединив законы Бойля-Мариотта и Гей-Люссака.
Уравнение Клапейрона, для данной массы газа
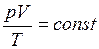 . (I.11)
. (I.11)
Для 2-х состояний
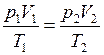 . (I.12)
. (I.12)
Русский учёный Д.И. Менделеев усовершенствовал уравнение Клапейрона, введя универсальную газовую постоянную 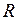 и постоянную Больцмана
и постоянную Больцмана 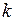 .
.
Уравнение Клапейрона-Менделеева (уравнение состояния идеального газа), для любой массы газа имеет вид
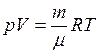 , (I.13)
, (I.13)
или
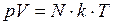 , (I.14)
, (I.14)
где 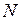 – число молекул;
– число молекул; 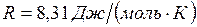 .
. 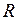 – универсальная газовая постоянная, ее можно определить как
– универсальная газовая постоянная, ее можно определить как 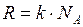 ,
,
где 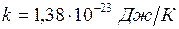 – постоянная Больцмана.
– постоянная Больцмана.
Дата добавления: 2016-09-06; просмотров: 4012;