Приближение линейными сплайнами
Пусть m = 1 .
Тогда общее число Q свободных параметров равно 2N .
Поставим вопрос о построении сплайна 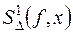 совпадающего с функцией f(x) в точках x0, x1,…, xn .
совпадающего с функцией f(x) в точках x0, x1,…, xn .
Получим систему уравнений

Эта система распадается на системы уравнений относительно коэффициентов отдельных многочленов
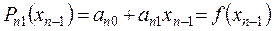 ,
,
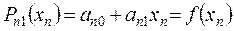
отсюда находим 
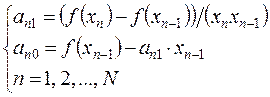
Многочлен Pn1(x) является многократно рассматривавшимся интерполяционным многочленом первой степени с узлами интерполяции xn-1, xn.
Широкое распространение сплайнов во многом вызвано тем, что они являются в определенном смысле наиболее гладкими функциями среди функций, принимающих заданные значения. Сплайны степени выше первой в случае гладкой f(x) хорошо приближают не только саму функцию, но и ее производные.
ЛЕКЦИЯ 9. ЧИСЛЕННОЕ ИНТЕГРИРОВАНИЕ ФУНКЦИЙ
Известно, что не для всякой функции ее первообразная выражается через элементарные функции. В этих случаях вычисление определенных интегралов по формуле Ньютона-Лейбница затруднительно и применяются различные методы приближенного вычисления определенных интегралов. Пользуясь геометрическим смыслом определенного интеграла, рассмотрим три приближенных формулы, с помощью которых численное интегрирование проводится с любой степенью точности.
Постановка задачи
Пусть на отрезке [a,b] задана непрерывная функция y = f(x). Требуется вычислить приближенное значение определенного интеграла
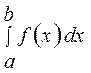 (9.1)
(9.1)
 Если f(x) ≥ 0 при a ≤ х ≤ b,то интервал будет численно равен площади так называемой криволинейной трапеции, ограниченной графиком функции y = f(x), прямыми х = a, х = b и осью Ох (рис.9.1).
Если f(x) ≥ 0 при a ≤ х ≤ b,то интервал будет численно равен площади так называемой криволинейной трапеции, ограниченной графиком функции y = f(x), прямыми х = a, х = b и осью Ох (рис.9.1).
Воспользуемся этой интерпретацией определенного интеграла.
Разобьем отрезок [a,b] точками a = х0, х1, ..., хn = b на n равных частей длины 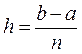 , так что xi = a + ih,
, так что xi = a + ih, 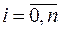 .
.
Величина h называется шагом интегрирования. Обозначим через у0, у1, …, уn значения функции y = f(x) в точках х0 , х1...., хn соответственно, то есть yi = f(xi), 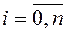 .
.
Дата добавления: 2021-09-07; просмотров: 579;











