Задача Коши. Общие замечания. Постановка задачи

Для дифференциального уравнения n-го порядка

уⁿ = f(x, у, у',…, у^(n-1)) (10.1)

задача Коши заключается в отыскании решения у = у(х) уравнения (10.1), удовлетворяющего начальным условиям

у(х₀) = у₀, у'(х₀)= у'₀, …, у^(n-1)(х₀)= у₀^(n-1),(10.2)

где х₀,у₀, у'₀, у₀^(n-1) – заданные числа. Если функция f (x,y,y',..., y^(n-1)) непрерывна, а ее частные производные 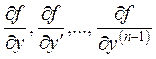ограничены в области, содержащей точку (х₀,у₀, у'₀, у₀^(n-1)), то существует единственное решение задачи Коши (10.1), (10.2).

Задача Коши для нормальной системы дифференциальных уравнений

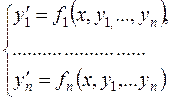(10.3)

заключается в отыскании решения y₁= y₁(x),…у_n = у_n(x)системы (10.3), удовлетворяющего начальным условиям

y₁(x₀)= у₁₀, у₂(x₀)= у₂₀, …, у_n(x₀)= у_n0 , (10.4)

где х₀, у₁₀, у₂₀, … у_n0– заданные числа. Если функции f(x, у₁,…, у_n), 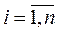непрерывны и имеют ограниченные частные производные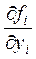 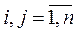в некоторой области, содержащей точку (х₀, у₁₀, у₂₀, … у_n0), то существует единственное решение задачи Коши (10.3), (10.4).

Известно, что систему дифференциальных уравнений, содержащую производные высших порядков и разрешенную относительно старших производных искомых функций, можно привести к системе вида (10.3) путем введения новых неизвестных функций. В частности, дифференциальное уравнение (10.1) порядка n приводится к системе вида (10.3) с помощью замены

у₁ = у', у₂ = у" , …, у _n-1= y ^(n-1),

что дает следующую систему

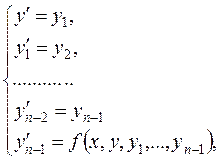(10.5)

то есть систему n дифференциальных уравнений первого порядка, правая часть которых не зависит от производных искомых функций. Поэтому численные методы решения дифференциальных уравнений традиционно изучают для уравнений первого порядка

а затем, как правило, без труда распространяют на нормальные системы дифференциальных уравнений вида (10.3). Так мы и поступим.

Итак, дано дифференциальное уравнение первого порядка, разрешенное относительно производной

y' = f(x,у),(10.6)

и начальное условие

у (х₀) = у₀ (10.7)

Требуется численно решить задачу Коши (10.6), (10.7) на отрезке [x₀, b]. Это решение будет состоять в построении таблицы приближенных значений у₁, у₂,…, у_n искомого решения у = у(х)в точках х₁, х₂, …, х_n = b, где y_i ≈ y (x_i),

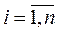. Для этого отрезок [x₀, b] делят на n равных частей длины 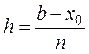, так что x_i = х₀+ih, 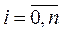. Величина h называется шагом интегрирования.

Метод Эйлера

Будем считать, что шаг интегрирования h настолько мал, что для всех 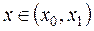значение искомой функции у(х) мало отличается от у₀. Тогда можно записать

у = у₀ + (х – х₀) f (х₀, у₀), .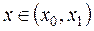

Иными словами, на этом участке интегрирования кривая у(х) заменяется отрезком касательной к ней в точке х₀.

Для х = х₁ получаем

у₁= у₀+ h∙f (x₀,y₀).

Аналогично для х = х₂можно получить

у₂ = у₁+ h∙f (x₁,y₁).

Продолжая строить дальнейшие значения приближенного решения по тому же закону, получим

y_i+1=y_i + h∙f (x_i, y_i), .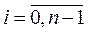

Используя известные обозначения, схему метода Эйлера можно представить формулами:

y_i+1= y_i +Δу_i, Δу_i = h∙f (x₁,y₁), 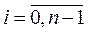(10.8)

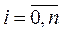Геометрический смысл метода Эйлера заключается в том, что искомая интегральная кривая у = у(х) заменяется ломаной, соединяющей точки М_i(x_i,y_i), (рис.10.1). Причем первое звено ломаной касается истинной интегральной кривой в точке М₀(х₀,у₀).

Эта ломаная называется ломаной Эйлера. При h→0 последовательность

ломаных Эйлера на отрезке [x₀, b] стремится к искомой интегральной кривой.

Оценку точности метода Эйлера, если неизвестно точное решение у = у(х), проводят с помощью двойного пересчета – с шагом h и с шагом 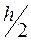. Совпадение десятичных знаков в полученных двумя способами результатах дает основание считать их верными.

Метод Эйлера легко распространяется на системы дифференциальных уравнений (10.3) и на дифференциальные уравнения высших порядков (10.1), которые должны быть предварительно приведены к нормальной системе (переход от (10.1) к (10.5)).

Рассмотрим систему двух дифференциальных уравнений первого порядка:

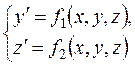(10.9)

с начальными условиями у(х₀)= у₀, z(x₀)= z₀. Приближенные значения у(x_i)≈ y_i, z(x_i)≈ z_i вычисляются последовательно по формулам:

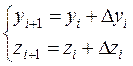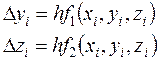
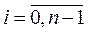, (10.10)

10.3. Модифицированный метод Эйлераявляется более точным методом по сравнению с предыдущим. Модификация метода направлена на то, чтобы более точно определить направление перехода из точки (x_i,y_i) в точку(x_i+1,y_i+1). Для чего производятся дополнительные промежуточные вычисления, в результате которых определяются координаты промежуточной точки

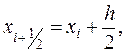
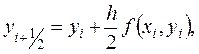(10.11)

с помощью которых и определяется следующее приближенное значение y_i+1 искомого решения по формуле

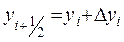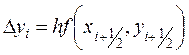, (10.12)

Геометрический смысл модифицированного метода Эйлера показан на рис.10.2. Исходя из точки М₀(x₀,y₀), получаем по методу Эйлера для х = 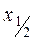точку .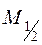

Для х = х₁ метод Эйлера дал бы точку 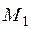на касательной кинтегральной кривой в точке М₀. Модифицированный метод состоит в том, что из точки М₀ проводится отрезок М₀М₁, параллельный отрезку 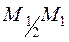, направленному в соответствии со значение углового коэффициента в точке 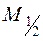. Точка М₁, которая получена по модифицированному методу Эйлера, находится ближе к истинной кривой, чем точка 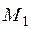. Следовательно, модифицированный метод Эйлера будет обеспечивать большую точность, чем метод Эйлера при одном и том же числе n разбиения отрезка интегрирования.

Модифицированный метод Эйлера легко распространить на нормальную систему дифференциальных уравнений (10.3). Рассмотрим систему двух уравнений первого порядка:

,

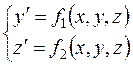с начальными условиями у₀ = у(х₀), z₀ = z(x₀).

Приближенные значения у(x_i) ≈ y_i, z(x_i) ≈ z_i вычисляются последовательно по формулам:

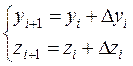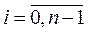, (10.13)

где ,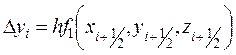

,

,

,

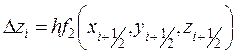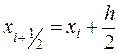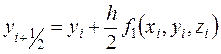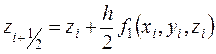
Метод Рунге-Кутта

Метод Рунге-Кутта – наиболее известный и широко используемый метод численного интегрирования обыкновенных дифференциальных уравнений. Метод Эйлера и модифицированный метод Эйлера можно рассматривать в качестве простейших представителей метода Рунге-Кутта или как упрощенные его варианты.

Согласно методу Рунге-Кутта, приближенные значения y_i+1 искомого решения у = у(х) определяются по формулам:

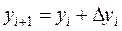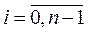, , (10.14)

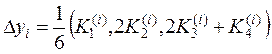, (10.15)

,

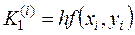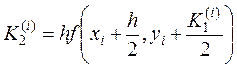, (10.16)

,

.

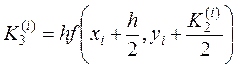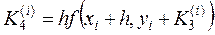Значение y_i+1 приближенного решения дифференциального уравнения (10.6) по методу Рунге-Кутта определяется в усредненном по формуле (10.15) направлении, составляющими которого являются четыре направления, определяемыми углами 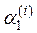, , 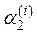, 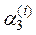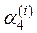для которых

, ,

, ,

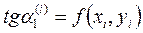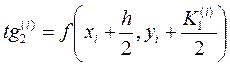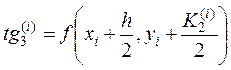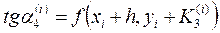что значительно повышает точность метода Рунге-Кутта. Для сравнения, в методе Эйлера y_i+1 вычисляется в направлении, определяемого углом φ_i , для которого tg φ_i = f(x_i,y_i) (рис.10.1). В модифицированном методе Эйлера y_i+1 вычисляется уже в подправленном с помощью средней точки текущего отрезка [x_i,x_i+1] направлении (рис.10.2), определяемом углом φ_i, для которого .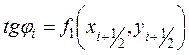

Метод Рунге-Кутта имеет порядок точности h⁴на всем отрезке [x₀, b]. Эффективная оценка погрешности метода очень затруднительна. Грубую оценку погрешности можно получить с помощью двойного просчета по формуле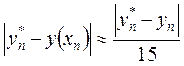

где у(х_n) – значение точного решения уравнения (1) в точке х_n а, 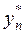– приближенные значения, полученные с шагом 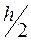и h.

Для определения правильности выбора шага h на практике применяют двойной просчет с шагом h и с шагом 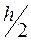. Если расхождение полученных значений не превышает допустимой погрешности, то шаг h для следующей точки удваивается, в противном случае берут половинный шаг.

Метод Рунге-Кутта обладает значительной точностью и, несмотря на свою трудоемкость, очень широко используется при численных решениях дифференциальных уравнений на ЭВМ. Важным преимуществом этого метода является возможность на любом этапе вычисления изменить шаг интегрирования, при условии выполнения заданной точности.

Распространим метод Рунге-Кутта на нормальную систему дифференциальных уравнений (10.3).

Рассмотрим систему двух дифференциальных уравнений первого порядка:

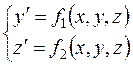
с начальным условием у₀ = у(х₀), z₀ = z(x₀).

Приближенные значения у(x_i) ≈ y_i, z(x_i) ≈ z_i вычисляются последовательно по формулам:

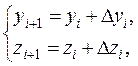
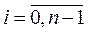(10.17)

где ; ;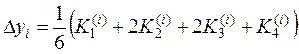

; ; ; ; ; ; ; .

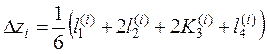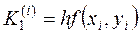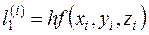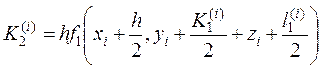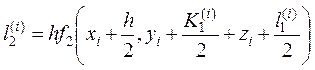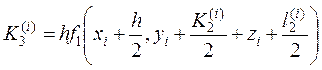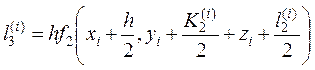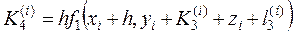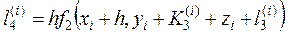ЛЕКЦИЯ 11. РАЗНОСТНЫЙ МЕТОД РЕШЕНИЯ УРАВНЕНИЙ МАТЕМАТИЧЕСКОЙ ФИЗИКИ (МЕТОД СЕТОК)

Разностный метод – это один из численных методов решения дифференциального уравнения, т.е. искомая функция получается в виде набора чисел.

Суть этого метода состоит в том, что искомый набор чисел получается при решении системы алгебраических уравнений, которые приближенно заменяют дифференциальные на некотором дискретном множестве, называемом сеткой.

Сеткой называется область дискретного изменения аргументов, на которую заменяют область непрерывного их изменения. Отдельные точки сетки называются узлами сетки.

Функция, определяемая в узлах сетки, называется сеточной функцией. Замена функции непрерывного аргумента сеточной функцией называется аппроксимацией.

Этот метод основан на замене производных разностными отношениями, так

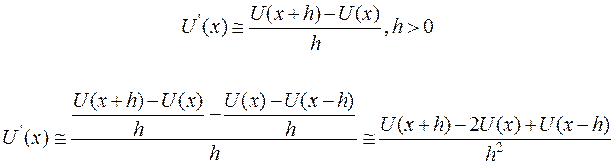
Близость разностного решения к точному зависит от выбора сетки. Основной целью всякого приближенного метода является получение решения исходной задачи с заданной точностью ε >0 за конечное число действий. Не любая конечно-разностная схема обеспечивает сходимость решения разностных уравнений к решению уравнения в частных производных. Такую сходимость решения обеспечивает лишь устойчивая схема.

Понятие устойчивости разностной схемы связано с ростом или затуханием ошибок, вносимых в расчет на любом этапе вычислений. Если разностная схема устойчива, то рост любого возмущения, вносимого на шаге n по времени, ограничен. Для неустойчивых конечно-разностных схем возмущение возрастает.

Разностная задача поставлена корректно при всех достаточно малых 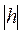, если:

1) решение разностной задачи существует и единственно для всех входных данных из некоторого дополнительного семейства;

2) решение непрерывно зависит от входных данных.

Свойство непрерывной зависимости решения разностной задачи от входных данных называется устойчивостью схемы по входным данным или просто устойчивостью.

Если схема устойчива и аппроксимирует исходную задачу, то она сходится, причем порядок точности (скорости сходимости) схемы определяется ее порядком аппроксимации. Отсюда следует, что изучение сходимости и порядка точности схемы сводится к изучению погрешности аппроксимации и устойчивости.

Рассмотрим идею разностного метода на конкретных примерах.