Метод сеток для уравнения параболического типа
Для задачи о распространении тепла в ограниченном стержне с теплоизолированной боковой поверхностью
Ut = a2·Uxx+g(x, t); 0 ≤ x ≤ l; t ≥ 0; (11.1)
(НУ) U(x,0) = f(x)(11.2)
(ГУ) U(0,t) = ф1(t); U(l,t) = ф2(t)(11.3)
Решение ищем в области, представляющей собой полуполосу на плоскости(x,у) (рис. 11.1). Примем для простоты, что a2 = 1 (этого всегда можно добиться, сделав замену переменных t1 = a2·t ).
Построим в области t ≥ 0, 0 ≤ x ≤ l прямоугольную сетку линиями x = xl и t = tj ,где xl = l ∙h (l=0, 1, 2, 3,….,n), tj = J ∙ τ (J = 0, 1, 2, 3,…), а h – шаг сетки по координате x, τ – шаг сетки по времени.

Рис.11.1
Станем рассматривать вместе непрерывной функции U(x, t) так называемую сеточную функцию Ul.,J = U(xl ,tJ), значения которой определены лишь в узлах сетки, т. е. точках (xl, tJ). В каждом внутреннем узле приближенно заменим производные Uxx , Ut соответствующими разностными отношениями.
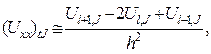
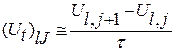 (11.4)
(11.4)
Обозначим g (xl,tJ ) = gl,.J, f(xl) = fl , ф1(t,J) = ф1,J , ф2(t,J) = ф2,J , где l = 0, 1, 2, 3,…. , n; j = 0, 1, 2,… .
Заменяя в уравнениях (11.1) - (11.3) функции U(x, t), g(x, t), f(x), ф1(t), ф2(t) сеточными функциями Ul,J, gl,J, ф1,J, ф2,J и производные конечно-разностными отношениями (11.4), получаем систему конечно-разностных уравнений:
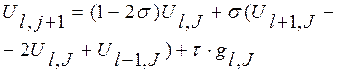 (11.5)
(11.5)
(НУ) Ut,,o = fl
(ГУ) Uo,J = ф1,J , Un,J = ф2,J ,
где t = 1,2,……, n; j = 0,1,….; ơ = τ/h2 – число Куранта.
Говорят, что уравнения (11.5)–(11.7) аппроксимируют. дифференциальное уравнение (11.1) с условиями (11.2) – (11.3). Таким образом, дифференциальное уравнение сводим к системе линейных алгебраических уравнений.
Если U (x, t)– точное решение краевой задачи, а Ul,J – точное решение конечно-разностных уравнений, то погрешность метода – это разность
εl,J = ׀Ul,J -U( l·h, j τ)׀ .
Возникают два вопроса:
1. Как ведет себя εl,J при J → ∞ и фиксированных h и τ ?
2. Как ведет себя εl,J, когда ячейки сетки измельчаются, т.е. h, τ → О при фиксированном J · τ.
Основная задача приближенных вычислений - указать способ, посредством которого погрешность можно сделать сколь угодно малой, так чтобы в пределе она стремилась к нулю. Как доказано, погрешность зависит от отношения скоростей, с которыми h и τ → 0.
Уравнения (11.5) - (11.7) связывают узловые точки по схеме, изображенной на рис.11.2 (явная схема).

Рис. 11.2
Зная значения сеточной функции Ul,J, на временном слое j, можно вычислить ее значения во внутренних точках на следующем временном слое j+1.
Из начальных условий (11.5) известны значения сеточной функции Ul,,j на временном слое j = 0, значения этой функции в граничных точках (0, j) и (n, j)известны из граничных условий (11.5). Так значения суточной функции Ul, ,J на временном слое j = 0 находятся из следующей системы уравнений
U0,1=ф1,l
U1,1=(1–2·ơ)·J1+ ơ·(J2+J0)+ τ·g1,0 ,
- - - - - - - - - - - - - - - - - - - - - - -
Ul,1=(1–2·ơ)·Jl+ ơ ·(Jl+1+Jl-1)+ τ·gl,0 ,
Un,1= ф2,l , где t=1, 2,……,n–1 .
Соотношение между шагами по х и t-ơ выбирается из условия обеспечения наибольшей точности. Доказано, что явная схема устойчива при ơ ≤ 0,5.
Наиболее простой вид уравнения (11.5) принимают при ơ = 0,5
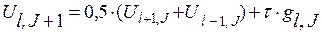 , (11.8)
, (11.8)
а при ơ= 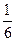
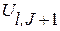 =
= 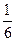 (
( 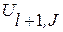 +
+ 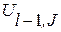 )+
)+ 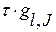 . (11.9)
. (11.9)
Если производную Ut в уравнении (11.1) заменить соотношением
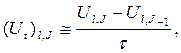
то получим неявную систему уравнений
(1+2·ơ)·Ul,J – ơ ·(Ul+1,J+ Ul-1,J)– Ul,J-1+ τ·gl,J = 0,(11.10)
связывающих узловые точки выбираем по схеме по схеме, изображенной на рис.11.3.
Рис.11.3
Непосредственный пересчет на новом временном слое теперь невозможен. Для решения разностных уравнений (11.10) используют специальные методы, например, метод прогонки, при этом объем вычислений возрастает примерно в пять-шесть paз no сравнению с явной схемой. Достоинство неявной схемы в ее абсолютной устойчивости. Она устойчива при любом значении числа Куранта (неявные схемы принято использовать при числе Куранта ơ ≥ 3).
ЛЕКЦИЯ 12. МЕТОД СЕТОК ДЛЯ УРАВНЕНИЯ ГИПЕРБОЛИЧЕСКОГО ТИПА
Метод сеток для уравнения гиперболического типа
Ut,t = a2·Uxx+g(x, t); 0 ≤ x ≤ l; t ≥ 0; (12.1)
(НУ) U(x,0) = f(x); Ut(x,0)=φ(x)(12.2)
(ГУ) U(0,t) = ф1(t); U(l,t) = ф2(t) (12.3)
аналогичен рассмотренному методу в (12.1), но требует знания начальных значений на двух временных слоях. Значение функции Ul,J на слое j = 0 известно из первого начального условия, а на слое j = 1 находим, используя второе начальное условие
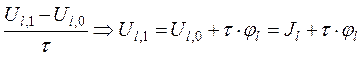 .
.
Система конечно-разностных уравнений для уравнения (12.1) с условиями (12.2)-(12.3) имеет вид
Ul,J+1 = 2·(1-r)·Ul,J+r·(Ul+1,J + Ul-1,J)- Ul,J-1+ τ2·gl,J (12.4)
(НУ) Ul,0= Jl; Ul,1 = Jl + τ·φl (12.5)
(ГУ) U0,J = ф1,J; Un,J = ф2,J (12.6)
где n = τ2/h2; J = 1,2,…,n; J = 1,2,….
Схема узловых точек изображена на рис. 12.1.
Рис. 12.1
Примечание. При граничных условиях второго и третьего рода, форму для расчета на границах получают, заменяя производные на границах на отношения конечных разностей.
Дата добавления: 2021-09-07; просмотров: 541;











