ВНДОХ (выплаты, начальное приближение)
Пусть R1 – выплата в конце первого периода, R2 – выплата в конце второго периода и т.д. Тогда ЧДД вычисляется по формуле
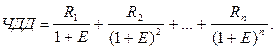 (62)
(62)
Если имеется выплата в начале первого периода R0, то она должна добавляться к ЧДД. Выплаты Ri могут иметь разные знаки и равняться нулю. Но процентная ставка Е и длина периодов неизменны.
Внутренняя доходность вычисляется Excel как решение уравнения
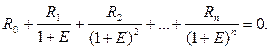 (63)
(63)
Уравнение может иметь несколько решений, поэтому последний аргумент ВНДОХ – начальное приближение.
Задача 24. Проект рассчитан на три года и требует начальных инвестиций в размере 10 млн руб. и имеет предполагаемые денежные поступления в размере 3 млн руб., 4 млн руб., 7 млн руб. Рассчитать ЧДД в предположении –ставки 10% и определить ВНД для этого проекта.
Решение:
Это типичная задача на оценку инвестиционных проектов. Покажем, что для расчета можно обойтись и без функции НПЗ.
| А | В | С | D | |
| ставка | 10% | |||
| Год | Выплата | ПЗ | ||
| -10 | -10 | =ПЗ(В1,А4,,-В4) | ||
| 2,727272727 | =ПЗ(В1,А5,,-В5) | |||
| 3,305785124 | =ПЗ(В1,А6,,-В6) | |||
| 5,259203606 | =ПЗ(В1,А7,,-В7) | |||
| 1,292261458 | =СУММ(С4:С7) | |||
| 1,292261458 | =НПЗ(В1,В5:В7)+В4 | |||
| 16,23% | =ВНДОХ(В4:В7) |
Каждый элемент потока платежей мы обрабатываем функцией ПЗ. В сумме получаем ЧДД. Тот же результат получен в ячейке С9.
Для того чтобы понять взаимодействие ЧДД и ВНД, построим таблицу значений ЧДД при различных %-ных ставках.
| А | В | |
| Ставка | ЧДД | |
| 0,0% | 4,00 | |
| 2,5% | 3,23 | |
| 5,0% | 2,53 | |
| 7,5% | 1,89 | |
| 10,0% | 1,29 | |
| 12,5% | 0,74 | |
| 15,0% | 0,24 | |
| 17,5% | -0,23 | |
| 20,0% | -0,67 |
 |
В ячейке В13 записана формула =НПЗ(А13,$B$5:$B$7)+$B$4 и скопирована вниз. На основе блока А12:В21 построим график (рис.12).
Рис.12. График зависимости ЧДД от Е
Из него видно, что чем выше %-ная ставка, тем меньше значение ЧДД. Например, при Е=20% значение ЧДД отрицательное. Это означает, что если бы мы положили в банк 10 млн руб. под 20% годовых, то на исходе 3-го года получили бы доход больше, чем в результате инвестиционного проекта.
Задача 25. Предлагаются 2 инвестиционных проекта, которые характеризуются предполагаемыми потоками платежей.
| Год | Проект А | Проект В |
| -100 | -100 | |
Сравнить инвестиционные проекты на основе ЧДД и ВНД.
Решение:
Постройте столбиковую диаграмму для потоков платежей. На первый взгляд, 2-ой проект выгоднее, т.к. сумма платежей для проекта А=60, а для проекта В = 70. Но так как платежи относятся к разным моментам времени, то с точки зрения финансового анализа результат арифметического сложения платежей не может служить критерием. Вычислим ВНД: для проекта А = 24%, а для проекта В = 21%. С точки зрения ВНД, проект А предпочтительнее.
Теперь рассчитаем ЧДД. Составим таблицу зависимости ЧДД от Е для обоих проектов (%-ная ставка изменяется от 0% до 30% с шагом 2,5%).
| А | В | С | D | E | F | G | |
| Год | Проект А | Проект В | Ставка | Проект А | Проект В | ||
| -100 | -100 | 0,0% | 60,00 | 70,00 | |||
| 2,5% | 51,18 | 58,37 | |||||
| 5,0% | 43,13 | 47,88 | |||||
| 7,5% | 35,79 | 38,39 | |||||
| 10,0% | 29,06 | 29,79 | |||||
| 12,5% | 22,87 | 21,96 | |||||
| ВНД: | 24% | 21% | 15,0% | 17,18 | 14,82 | ||
| 17,5% | 11,92 | 8,29 | |||||
| 20,0% | 7,06 | 2,31 | |||||
| 22,5% | 2,55 | -3,17 | |||||
| 25,0% | -1,63 | -8,22 | |||||
| 27,5% | -5,53 | -12,88 | |||||
| 30,0% | -9,16 | -17,18 | |||||
| Точка | |||||||
| Фишера | 11,07% | 26,34 | 26,34 | ||||
| 0,0 |
Перечислим формулы:
В В8 =ВНДОХ(В2:В6), формула скопирована в С8. В
F2 =НПЗ($Е2,В$6)+В$2. Эта формула скопирована в блок F2:G14. Для блока Е1:G14 строим линейный график. По диаграмме выясняем, что графики пересекаются при величине ставки 11%. Более точное значение определяем с помощью команды «Сервис/Подбор параметра» (в
F16 =НПЗ($E16,B$3:B$6)+B$2, в G17 =F16-G16, в Е16 помещаем начальное приближение 11%). Точка пересечения графиков носит название точки Фишера. При Е<11% выгоднее проект В, а при Е>11% - проект А.
Дата добавления: 2019-09-30; просмотров: 991;











