ДВУХГРУППОВОЕ ДИФУЗИОННОЕ ПРИБЛИЖЕНИЕ

Стационарное пространственное распределение тепловых нейтронов N (r) описывается уравнением диффузии

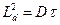; , (8.172)

где Q( ) — плотность замедления надтепловых нейтронов, являющаяся распределенным в пространстве источником тепловых нейтронов.

Решение этого уравнения следующее:

, (8.173)

где 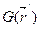— функция Грина уравнения диффузии для бесконечной однородной среды имеет вид

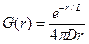. (8.174)

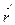Если поле нейтронов рассматривается в веществе, для которого выполняется неравенство ( — полный возраст нейтронов), то распределение тепловых нейтронов должно повторять распределение надтепловых (поглощение происходит вблизи места их рождения). В этом случае диффузионное ядро G(r) очень быстро убывает с увеличением разности . Представив плотность замедления нейтронов Q( ) в окрестности точки разложением

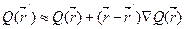, (8.175)

подставив выражение (96) в (95) и учтя неравенство 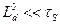, получим (выполнив интегрирова­ние):

, (8.176)

Из выражения (90) вытекает возможность оценки среднего времени жизни тепловых нейтронов 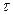по результатам измерений пространственного распределения надтепловых и тепловых нейтронов от стационарного источника (в однородной безграничной среде).

Рис.8.23. Обратная величина «кадмиевого отношения» в скважине как функция массового сечения поглощения (по Е.И. Крапивскому).

Поскольку для стационарного источника плотность замедления Q(r) приближенно пропорциональна плотности 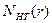надтепловых нейтронов, то, вычислив отношение 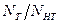, получим

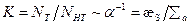, (8.177)

(эта величина определяется по так называемому «кадмиевому отношению», представляющему собой отношение показаний двух счетчиков, один из которых экранирован кадмиевой фольгой). Величина пропорциональна макроскопическому сечению поглощения среды и, следовательно, линейно зависит от концентрации поглотителя. Этот практически важный вывод подтверждается результатами экспериментальных измерений в скважинах. На рис.8.23 приведена зависимость величины от массового сечения поглощения, нормированная к нулевой концентрации поглотителя (бор). Измерения выполнены в необсаженной скважине диаметром 60 мм прибором диаметром 40 мм; размер зонда 25 см; источник 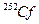; счетчик нейтронов — СНМ-16 с борной экранировкой от заполнения скважины. Возможность перехода к эквивалентной по сечению поглощения (см. раздел 6.2) концентрации позволяет прокалибровать эту зависимость по концентрации любого поглотителя.

Распределение надтепловых нейтронов практически нечувствительно к изменению сечения поглощения среды (в частности, к изменению минерализации пластовой жидкости), поэтому соотношение (90) позволяет оценить изменение плотности тепловых нейтронов в. переходной зоне водонефтяного контакта (без учета влияния скважины, уменьшающего дифференциацию). Учитывая, что в пласте-коллекторе изменение характера флюида, насыщающего поровое пространство (при неизменной пористости и при измерениях на фиксированном размере зонда), обусловливает лишь изменение времени жизни тепловых нейтронов при постоянстве водородосодержания, получаем:

,

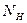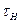где и , и — плотности и времена жизни тепловых нейтронов в нефтеносной и водоносной частях коллектора соответственно.

Рассмотрев пространственное распределение замедляющихся нейтронов в одногрупповом диффузионном приближении, и подставив (34) в (88), получим

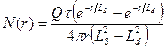. (8.178)

Справедливость выражения (92), полученного в двухгрупповом диффузионном приближении, для описания пространственного распределения тепловых нейтронов от точечного источника быстрых нейтронов была подтверждена экспериментами с Рu-Ве -источником нейтронов в водных растворах окиси бора при различных температурах (от 35 до 75 °С) и различных концентрациях поглотителя (до 80 г/л).

Средний квадрат расстояния, проходимого нейтронами в процессе замедления и диффузии до поглощения, определяет важную нейтронную характеристику среды, называемую площадью миграции нейтронов :

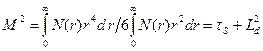. (8.179)

При совпадении длин замедления и диффузии, когда Ls = Ld = 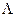, получаем (раскрыв неопределенность типа 0/0 по Лопиталю)

, (8.180)

Величина 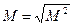называется длиной миграции. Знание этой величины позволяет описывать пространственное распределение тепловых нейтронов от источника быстрых нейтронов в одногрупповом диффузионном приближении. Для изучения закономерностей распределения тепловых нейтронов в системе прибор — скважина — пласт удобнее пользоваться не длиной миграции М, аобратной ей величиной :

.

Из выражения (92) следует, что на больших расстояниях от источника быстрых нейтронов пространственное распределение тепловых нейтронов зависит от свойств среды или через длину замедления или через длину диффузии 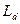в зависимости от того, какой из этих параметров обладает наибольшей величиной. Поскольку в водоносных породах, насыщенных минерализованной пластовой жидкостью, длина диффузии всегда меньше длины замедления, на достаточно больших расстояниях выражение (92) можно с хорошим приближением заменить выражением

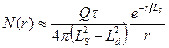. (8.178')

Отношение A(r₁,r₂) плотностей тепловых нейтронов, измеренных на двух различных (но достаточно больших) расстояниях от источника 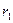и уже не зависит от нейтронных характеристик среды для тепловых нейтронов (а также мощности источника):

Величина этого отношения весьма чувствительна к изменению водородосодержания и более стабильна по отношению к изменениям минерализации пластовой воды и типа горной породы.. Этот вывод остается справедливым и в условиях скважинных измерений. При рассмотрении отношения A(m) как интерпретационного параметра ННМ в двухзондовой модификации (ННМ-2), он приобретает одно важное и нетривиальное качество. Таковым является механизм автоматической помехоустойчивости к неконтролируемым изменениям параметров «ближней зоны», каковыми являются изменения диаметра скважины, эксцентриситет прибора, и др. Однако обосновать это свойство мы сможем только тогда, когда изучим закономерности полей нейтронов в системе скважина-пласт.