ВОЗРАСТНОЕ ПРИБЛИЖЕНИЕ
Источник нейтронов будем считать изотропным, стационарным и точечным с единичной мощностью. Во всем пространстве, кроме области, занимаемой источником в начале координат, 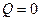 .
.
Предположим, что кинетическая энергия 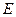 замедленных нейтронов много меньше их начальной энергии
замедленных нейтронов много меньше их начальной энергии 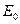 . В этом случае нейтроны должны испытать в среднем большое число столкновений с ядрами замедлителя, вследствие чего функция распределения
. В этом случае нейтроны должны испытать в среднем большое число столкновений с ядрами замедлителя, вследствие чего функция распределения 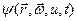 с уменьшением энергии теряет свою угловую анизотропию. Угловая зависимость поэтому может быть представлена в виде двух первых членов разложения ее в ряд по сферическим функциям:
с уменьшением энергии теряет свою угловую анизотропию. Угловая зависимость поэтому может быть представлена в виде двух первых членов разложения ее в ряд по сферическим функциям:
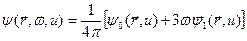 , (8.70)
, (8.70)
где 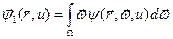
- поток нейтронов, деленный на длину свободного пробега, или первый угловой момент функции распределения. При этом предполагается выполнение неравенства:
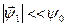 , (8.71)
, (8.71)
означающего слабую пространственную зависимость функции распределения нейтронов.
Подставляя разложение (8.70) в уравнение переноса (8.67), и интегрируя по углам, получим:
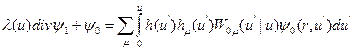 (8.72)
(8.72)
Умножая далее уравнение переноса на  и интегрируя по углам, имеем:
и интегрируя по углам, имеем:
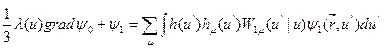 (8.72
(8.72  )
)
Уравнения (8.72) и (8.72) образуют систему, позволяющую определить функции 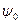 и
и 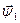 . Фазовое распределение нейтронов восстанавливается по этим функциям в соответствии с формулой (8.70).
. Фазовое распределение нейтронов восстанавливается по этим функциям в соответствии с формулой (8.70).
Предположим, что произведение 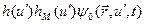 слабо зависит от изменения летаргии в интервале
слабо зависит от изменения летаргии в интервале 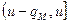 , вследствие чего в интеграле столкновений оно может быть аппроксимировано начальными членами тэйлоровского разложения по летаргии:
, вследствие чего в интеграле столкновений оно может быть аппроксимировано начальными членами тэйлоровского разложения по летаргии:
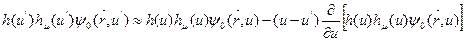 .
.
Примем также, что 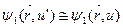 . Тогда система уравнений (8.72) и (8.72') принимает следующий вид:
. Тогда система уравнений (8.72) и (8.72') принимает следующий вид:
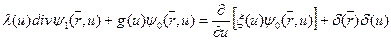 ; (8.73)
; (8.73)
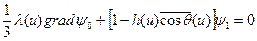 . (8.73')
. (8.73')
В уравнении (8.73) использовано определение среднего изменения летаргии 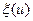 , а в уравнении (8.73')—среднего косинуса угла рассеяния
, а в уравнении (8.73')—среднего косинуса угла рассеяния 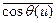 .
.
Из выражения (8.73) следует уравнение, называемое законом Фика:
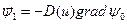 , (8.74)
, (8.74)
где D(u) – коэффициент диффузии для плотности потока
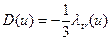 . (8.75)
. (8.75)
Величина
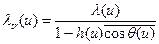 (8.76)
(8.76)
называется транспортной длиной свободного пробега или длиной переноса. Она характеризует длину свободного пробега нейтронов с учетом их преимущественного рассеяния в переднюю полусферу из-за угловой анизотропии однократного столкновения.
Подставляя (8.74) в уравнение (8.73), получим:
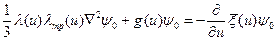 . (8.77)
. (8.77)
Таким образом, интегро-дифференциальное уравнение переноса преобразовано в дифференциальное уравнение в частных производных второго порядка параболического типа относительно функции 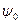 .
.
Напомним, что уравнение (8.77) получено, исходя из предположений о том, что индикатриса рассеяния обладает слабой анизотропией, функция углового распределения нейтронов слабо зависит от координат
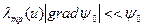 , (8.78)
, (8.78)
и что произведение 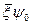 слабо зависит от летаргии (это значительно менее жесткое ограничение, чем предположение о слабой энергетической зависимости непосредственно величины
слабо зависит от летаргии (это значительно менее жесткое ограничение, чем предположение о слабой энергетической зависимости непосредственно величины 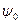 ):
):
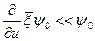 . (8.79)
. (8.79)
Указанные условия предполагают выполнение неравенств
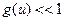 , или
, или 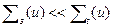 , (8.80)
, (8.80)
(очень слабое поглощение), поскольку присутствие в замедлителе поглощающих нейтроны примесей существенно усиливает пространственную и энергетическую зависимость функции распределения, а также ее угловую анизотропию.
Дифференциальное уравнение (8.77) можно упростить подстановкой
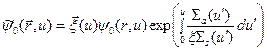 (8.81)
(8.81)
и введением вместо летаргии 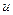 новой переменной
новой переменной 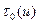
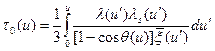 . (8.82)
. (8.82)
В этом случае оно принимает вид
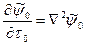 , (8.83)
, (8.83)
т. е. совпадает с уравнением теплопроводности, в котором роль времени играет переменная 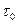 (при этом коэффициент температуропроводности равен единице). Величина
(при этом коэффициент температуропроводности равен единице). Величина 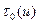 имеет размерность площади и называется «фермиевским возрастом» нейтронов, а уравнение (8.83) - «уравнением возраста».
имеет размерность площади и называется «фермиевским возрастом» нейтронов, а уравнение (8.83) - «уравнением возраста».
Решение уравнения (8.83) имеет следующий вид:
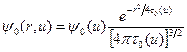 , (8.84)
, (8.84)
где
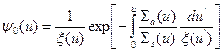 . (8.85)
. (8.85)
Решение уравнения (8.83) получено в предположении слабой зависимости 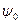 от координат
от координат
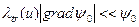 или
или 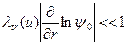 (8.86)
(8.86)
и слабой зависимости произведения 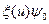 от летаргии (это менее жесткое ограничение, чем предположение о слабой энергетической зависимости непосредственно
от летаргии (это менее жесткое ограничение, чем предположение о слабой энергетической зависимости непосредственно 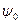 ):
):
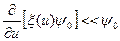 . (8.87)
. (8.87)
Указанные условия предполагают в свою очередь выполнение неравенства g(u)<<l или 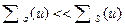 , поскольку присутствие поглотителей нейтронов существенно усиливает пространственную, угловую и энергетическую зависимость функции распределения. По этой причине выражение (21) применимо для описания энергетического спектра нейтронов, замедленных лишь в слабо поглощающих средах.
, поскольку присутствие поглотителей нейтронов существенно усиливает пространственную, угловую и энергетическую зависимость функции распределения. По этой причине выражение (21) применимо для описания энергетического спектра нейтронов, замедленных лишь в слабо поглощающих средах.
Подставляя (8.84) в (8.86), находим
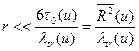 , (8.88)
, (8.88)
где 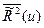 — средний квадрат смещения нейтрона в процессе замедления до заданной энергии. Следовательно, выражение (8.84) справедливо на малых расстояниях от источника. Из условия (8.87) следует
— средний квадрат смещения нейтрона в процессе замедления до заданной энергии. Следовательно, выражение (8.84) справедливо на малых расстояниях от источника. Из условия (8.87) следует 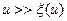 , т. е. заданное значение летаргии должно достигаться в результате большого числа столкновений
, т. е. заданное значение летаргии должно достигаться в результате большого числа столкновений 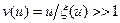 . При этом условии анализ результата возрастного приближения как частного случая строгого решения уравнения переноса дает более точную оценку границ применимости. Выражение (21) справедливо до расстояний порядка
. При этом условии анализ результата возрастного приближения как частного случая строгого решения уравнения переноса дает более точную оценку границ применимости. Выражение (21) справедливо до расстояний порядка 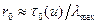 , где
, где 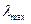 — максимальная на интервале замедления полная длина свободного пробега нейтронов.
— максимальная на интервале замедления полная длина свободного пробега нейтронов.
«Исправление» возрастного приближения
Из выражений (8.86) и (8.88) видно, что выражение (8.84) справедливо лишь на малых расстояниях от источника нейтронов, особенно для сред повышенного водородсодержания. На больших расстояниях оно дает качественно неверную пространственную зависимость. Это обусловлено не только допущениями возрастного приближения, но и некорректностью представления о «точечности» источника нейтронов с начальной энергией Е0.
Нейтроны, испускаемые точечным источником, сохраняют начальную энергию 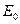 до первого столкновения с ядрами замедлителя, проходя в веществе путь, равный среднему свободному пробегу
до первого столкновения с ядрами замедлителя, проходя в веществе путь, равный среднему свободному пробегу 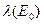 , вследствие чего они распределены в пространстве по некоторому закону (закону распределения нерассеянного излучения). Пространственно-угловое распределение
, вследствие чего они распределены в пространстве по некоторому закону (закону распределения нерассеянного излучения). Пространственно-угловое распределение 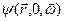 нерассеянных нейтронов, сохранивших в замедлителе свою энергию, описывается уравнением переноса (8.51), в котором отсутствует интеграл столкновений
нерассеянных нейтронов, сохранивших в замедлителе свою энергию, описывается уравнением переноса (8.51), в котором отсутствует интеграл столкновений 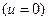 :
:
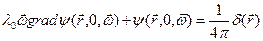 . (8.89)
. (8.89)
Решение этого уравнения относительно нулевого углового момента имеет вид
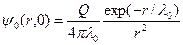
и определяет пространственное распределение замедленных нейтронов на больших расстояниях:
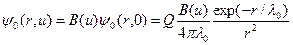 , (8.90)
, (8.90)
где 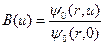 - «фактор накопления» замедленных нейтронов.
- «фактор накопления» замедленных нейтронов.
На «средних» расстояниях от источника 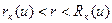 пространственное распределение замедленных нейтронов описывается значительно более сложно. Согласно общей теории, в этой области функция распределения задается параметрически [ ].
пространственное распределение замедленных нейтронов описывается значительно более сложно. Согласно общей теории, в этой области функция распределения задается параметрически [ ].
Для изучения физических закономерностей вне области применимости возрастного приближения применяется «одногрупповое диффузионное приближение» (см. ниже).
В возрастном приближении свойства вещества описываются одним параметром — фермиевским возрастом τ0. Чем сильнее замедлитель, чем больше его водородосодержание[2], тем меньше величина τ0. Выражение (8.84) показывает, что зависимость показаний детектора надтепловых нейтронов от водородосодержания среды с изменением расстояния до источника (размера зонда) изменяется.
На малых расстояниях, например, на «нулевом» зонде
N0(m) ~ τ0(m)-3/2, (8.91)
зависимость от m возрастающая. На больших расстояниях r зависимость от m определяется экспонентой
N0(m) ~ exp[- r2/4τ0(m)], (8.92)
и зависимость становится убывающей (Рис.7.14).
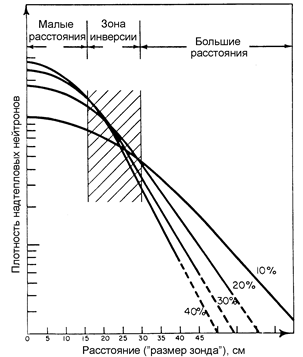 Рис.8.1. Эффект инверсии зависимости показаний ННМнт от водородосодержания с изменением размера зонда (по Дж. Титтмену).
Рис.8.1. Эффект инверсии зависимости показаний ННМнт от водородосодержания с изменением размера зонда (по Дж. Титтмену).
В геофизике переменное водородосодержание является изучаемой величиной (аргументом), связанной с ФЕС коллекторов нефти и газа, а расстояние между источником и детектором — управляемым параметром. Изменение (обращение) функции с растущей на убывающую с изменением параметра называется инверсией или инверсионным эффектом. Зона расстояний, на которых зависимости N0(m) обладают минимальной чувствительностью к m, является инверсионной, и делит зависимости N0(m) и соответствующие зонды на доинверсионные (растущие по m показания) и заинверсионные (убывающие по m показания).
«Теоретические» и феноменологические уравнения поля
Уравнение переноса описывает закономерности переноса вещества в различных его формах. Закон Фика для диффундирующих частиц (в частности, молекул, нейтронов, гамма-квантов) является одним из основных законов физической кинетики. Его формулировка:
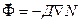 , (8.93)
, (8.93)
означает, что поток частиц 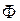 в единицу временипропорционален плотности (концентрации) частиц N и направлен в сторону, противоположную градиенту; коэффициент диффузии Д является коэффициентом пропорциональности (Д = Dv). Этот закон был установлен немецким физиологом А.Фиком (1855) экспериментально.
в единицу временипропорционален плотности (концентрации) частиц N и направлен в сторону, противоположную градиенту; коэффициент диффузии Д является коэффициентом пропорциональности (Д = Dv). Этот закон был установлен немецким физиологом А.Фиком (1855) экспериментально.
Приведенный выше вывод этого закона является теоретическим, устанавливающим одновременно ограниченность области его применимости. Можно привести ряд аналогов этого закона, установленных феноменологически для переноса вещества в различных его формах.
Для электрического тока (движения электрических зарядов) аналогом закона Фика является законом Ома (в дифференциальной форме):
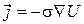 , (8.94)
, (8.94)
где j — плотность тока (сила тока, приходящегося на единицу поперечного сечения проводника), s – проводимость, U — потенциал, следует, что коэффициент диффузии нейтронов играет роль «нейтронной проводимости» вещества: чем больше коэффициент диффузии, тем меньше «сопротивление» замедлителя прохождению нейтронов данной энергии.
Для теплового поля тепловой поток определяется законом Фурье
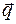 = – l grad T,(8.95)
= – l grad T,(8.95)
где 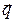 – вектор плотности теплового потока, l –коэффициент теплопроводности, для изотропной среды являющийся скаляром.
– вектор плотности теплового потока, l –коэффициент теплопроводности, для изотропной среды являющийся скаляром.
Для жидкости, фильтрующейся в пористой среде, аналогом (8.93) является закон Дарси:
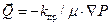 , (8.96)
, (8.96)
где 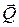 – количество жидкости с динамической вязкостью m, прошедшей через единицу поверхности среды в единицу времени; kпр – коэффициент проницаемости среды; P – давление.
– количество жидкости с динамической вязкостью m, прошедшей через единицу поверхности среды в единицу времени; kпр – коэффициент проницаемости среды; P – давление.
Во всех рассмотренных примерах перенос вещества обусловлен наличием градиентов (концентрации, электрических потенциалов, температуры, давления).
Дата добавления: 2020-08-31; просмотров: 792;











