Диффузия и диффузионное приближение. Уравнение диффузии.

При энергиях ~ 1 эВ и ниже устанавливается спектр тепловых нейтронов. При этих энергиях скорость движения нейтронов сопоставима с движением ядер среды. Движение тепловых нейтронов в среде не сопровождается изменением их средней энергии. В процессе хаотического движения тепловых нейтронов они претерпевают рассевающие соударения с ядрами среды (также находящимися в состоянии хаотического движения), в результате чего энергия нейтронов то уменьшается, то увеличивается, колеблясь около некоторого среднего наиболее вероятного значения. Распределение нейтронов по скоростям (энергиям) подчиняется распределению Максвелла, установленному для состояния термодинамического равновесия газов. Процесс установления спектра тепловых нейтронов под влиянием теплового движения атомов среды называют термализацией нейтронов.

Установившийся спектр тепловых нейтронов (спектр Максвелла), находящихся в тепловом равновесии со средой, представляет собой поле свободных нейтронов. Их поведение описывается уравнением газовой кинетики. Температура нейтронного газа (Т_н.г.) совпадает с температурой среды Т. В первом приближении в гомогенной среде

Т_н.г. » Т(1+1,4S_а(Т)/xS_s), [К].

Процесс рассеяния тепловых нейтронов при постоянстве их средней энергии называют диффузией нейтронов. В процессе диффузии нейтроны смещаются из области с большей плотностью нейтронов в область с меньшей. При определенных допущениях основные положения теории диффузии газов могут быть использованы для описания пространственного смещения тепловых нейтронов.

Распространение нейтронов в среде можно рассматривать аналогично процессу диффузии газа в атмосфере и применять закон Фика и уравнение диффузии.

Диффузионное приближение справедливо только при следующих условиях:

- нейтрон рассматривается как точечная частица и пренебрегается нейтрон-нейтронным взаимодействием, считается, что энергия тепловых нейтронов практически не меняется при столкновениях с ядрами среды;

- ядра среды должны быть достаточно тяжелыми для обеспечения изотропного рассеяния (для поправки на анизотропность рассеяния вводят транспортные величины);

- макроскопические сечения рассеяния должны быть неизменными или, в крайнем случае, слабо зависеть от пространственных координат (это означает, что в однородных средах, например, в протяженном чистом замедлителе, поле нейтронов не зависит от направления, от угловых переменных);

- среда не должна содержать сильно локализованных источников или поглотителей нейтронов, поток нейтронов должен слабо меняться на длине свободного пробега нейтрона (слабопоглощающая среда Σ_s >> Σ_a, области вдали от источников или границ раздела сред).

В ряде областей, например, вблизи границы среды (тела) с пустотой (воздух для нейтронов), сильного поглотителя, источника нейтронов и т.п. диффузионное приближение плохо описывает действительность. При значительных отклонениях ищут решение не уравнения диффузии, а кинетического уравнения. Если объем этих областей мал по сравнению с полным объемом среды, то вводятся поправки к решению уравнения диффузии.

При решении уравнения диффузии всегда рассматривается «средний» нейтрон.

Плотность потока нейтронов Ф можно определить как число нейтронов DN пересекающих в единицу времени Dt единицу площади DS:

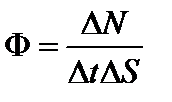[см^-2×с^-1 или нейтр./(см²×с)].

Всегда происходит направленное перемещение нейтронов из области с большей плотностью потока нейтронов Ф в область с меньшей плотностью потока нейтронов Ф. Это смещение происходит против направления градиента плотности потока нейтронов пропорционально коэффициенту диффузии среды D и описывается векторной величиной – током нейтронов (закон Фика).

Ток нейтронов 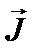– вектор, имеющий в каждом направлении проекцию, равную суммарному числу нейтронов, пересекающих единичную поверхность, перпендикулярную этому направлению в единицу времени для данного значения энергии, времени и с учетом встречных направляющих плотности потока Ф в данной точке. Результирующий ток нейтронов описывается законом Фика:

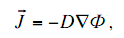
где D – коэффициент диффузии нейтронов, D = λ_tr/3, λ_tr – транспортный пробег.

Отсюда следует, что диффузионный ток – это вектор, показывающий в каком направлении и сколько нейтронов в данной точке пространства в единицу времени пересекает единицу площади вследствие встречных составляющих плотности потока Ф по этому направлению.

Если в какой-то области пространства нейтронная плотность не зависит от пространственных координат, то 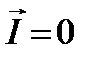, тогда как Ф=nv.

Замедляясь и диффундируя, нейтроны взаимодействуют с ядрами размножающей среды и перемещаются от места рождения.

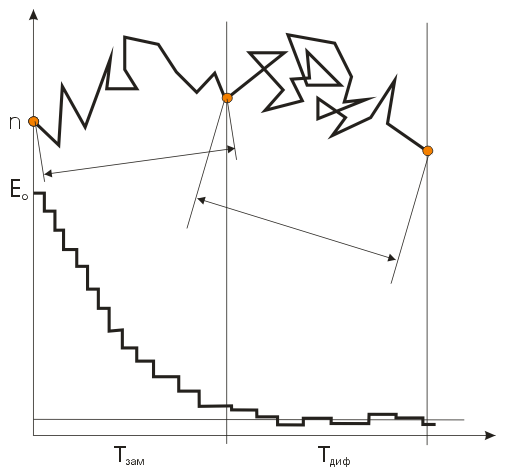
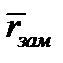
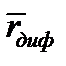
Рис. 1.5. Схема замедления и диффузии нейтронов

Поскольку процессы рассеяния и поглощения независимы:

,

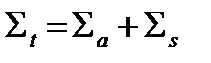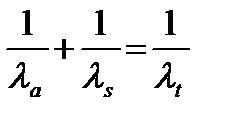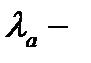то , где средняя длина свободного пробега нейтронов до поглощения; 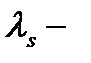средняя длина свободного пробега до рассеяния;

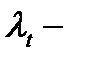средняя длина свободного пробега до первого столкновения.

Если 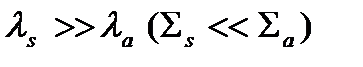, то большая часть столкновений нейтрона с ядрами среды приводит к захвату нейтрона. Такая среда называется сильнопоглощающей.

Если 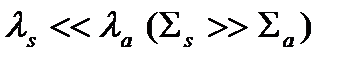, среда называется слабопоглощающей.

Случай несимметричного (анизотропного) рассеяния приводится к случаю сферической симметрии введением транспортной длины свободного пробега нейтрона 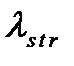, которая представляет собой эффективное смещение нейтрона в направлении движения до следующего акта рассеяния, которому соответствует поворот траектории нейтрона на угол .

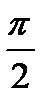Средняя длина свободного пробега 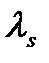, исправленная на не сферичность рассеяния, называется транспортной длинной свободного пробега в отсутствии поглощения. В соответствии с этим вводится понятие транспортного макроскопического сечения:

,

,

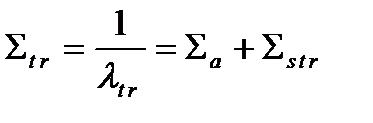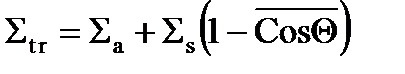где 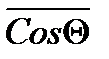средний косинус угла рассеяния. Используется в качестве угловой характеристики акта рассеяния.

Альбедо b – отражательная способность (поверхности среды) с учетом (3.8) и (3.11)

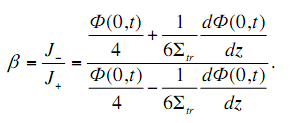(3.16)

Скорость утечки нейтронов Р [нейтр./см³с] – это число нейтронов, уходящих из единичного объема среды за 1 с.

Как было сказано выше для осуществления контролируемой ЦР в ЯР необходимо поддерживать баланс нейтронов. Баланс нейтронов в единице объема определяется тремя процессами:

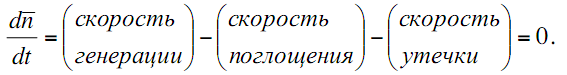
Скорость генерации нейтронов [нейтр./см³×с] – число нейтронов, появляющихся (рождаемых) в единицу времени в единичном объеме 1 см³ – можно записать как функцию .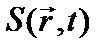

Скорость поглощения [нейтр./см³×с] – число нейтронов, поглощаемых в единицу времени в единичном объеме 1 см³ среды – можно записать в виде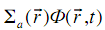

Скорость утечки описывается выражением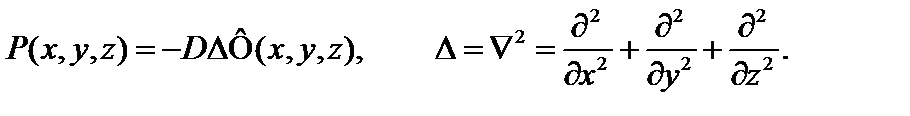

Подставляя в условие баланса нейтронов выражения для скоростей генерации 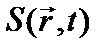, поглощения 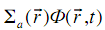и утечки нейтронов, получим уравнение диффузии нейтронов для среды, свойства которой изменяются плавно

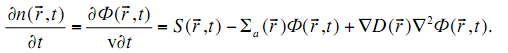(3.21)

При скачкообразном (резком) изменении свойств, например, на границах сред, необходимо для каждой среды записывать это уравнение с соответствующими граничными условиями. Для однородной среды, свойства которой не зависят от координат

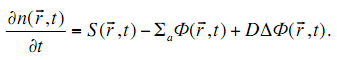(3.22)

Уравнение диффузии для стационарной задачи (нет переменной времени)

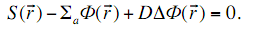(3.23)

Нейтроны различных энергий распределены в активной зоне ЯР по-разному. Плотность потока нейтронов напрямую определяет число делений и, следовательно, энерговыделение в каждой области активной зоны ЯР. Для управления ЯР необходимо знать плотность потока нейтронов 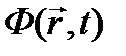как функцию координат и времени, удовлетворяющую, в простейшем случае, диффузионному приближению моноэнергетических нейтронов. Эта функция однозначно определяется из ряда дополнительных (начальных и граничных) условий, которым она должна удовлетворять по физическому смыслу в каждой конкретной задаче теории диффузии нейтронов:

1. Условие на выпуклой границе среды с вакуумом.Диффузионное приближение плохо описывает распределение плотности потока нейтронов в окрестностях границы среды с вакуумом, так как на границе резко меняются свойства сред.

В связи с этим, односторонний ток нейтронов из вакуума в среду равен нулю.

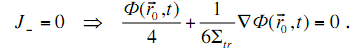. (3.24)

Где, 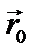вектор, определяющий положение пространственных точек выпуклой границы среды с вакуумом

Условие (3.24) справедливо для «голого» реактора – реактора без отражателя. Введем параметр – длину линейной экстраполяции

.

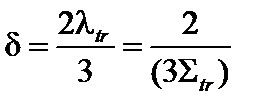d – это расстояние от реальной границы тела (среды), на котором происходит обращение экстраполированного потока нейтронов в нуль

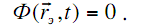(3.30)

Формулу (3.30) называют условием для плотности потока нейтронов на экстраполированной границе среды с вакуумом.

2. Условия сшивки решений уравнения диффузии на границе раздела сред с различными нейтронно-физическими свойствами. Если рассматриваемая активная зона (тело) состоит из нескольких сред, то для простоты считают, что свойства сред не зависят от координат внутри этих сред, а изменяются лишь на их границах. Количество нейтронов, вылетающих в единицу времени из одной среды должно равняться количеству нейтронов, влетающих в единицу времени в другую среду, и наоборот (равенство односторонних токов).

Условия сшивки решений имеют вид:

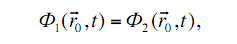(3.31)

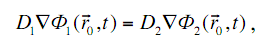(3.32)

где D_i (i = 1, 2) – коэффициенты диффузии соответствующих сред. По сути, (3.31), (3.32) – требования непрерывности плотности потока нейтронов и проекций на нормаль к границе раздела плотности тока нейтронов при переходе границы раздела сред.

3. Условие локализованных источников.

Условие локализованного источника имеет вид:

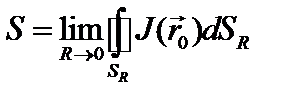. (3.33)

Это условие следует понимать как равенство числа испускаемых источником в единицу времени нейтронов числу нейтронов, утекающих сквозь поверхность элементарной сферы с источником в центре при ее радиусе, стремящемся к нулю.

4. Условие ограниченности и неотрицательности нейтронного потока.Согласно физическому смыслу нейтронный поток не может быть бесконечно большим и отрицательным, т.е.

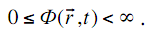(3.34)

5. Начальные условия в нестационарных задачах.Для решения нестационарного уравнения, необходимо знать распределение плотности потока нейтронов в момент времени t = 0:

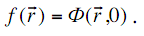(3.35)

6. Условия, определяемые геометрическими и физико-химическими особенностями решаемой задачи.Сложные задачи решаются достаточно просто аналитически, например, при наличии симметрии в системе, при разбиении сложной системы на части, при группировке составляющих сложных систем по схожести свойств, например, метод гомогенизации реакторной ячейки и т.д.

Стационарное уравнением диффузии моноэнергетических нейтронов в форме (3.23):

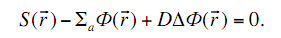
Считая, что коэффициент диффузии 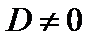, разделим обе части уравнения на D, тогда уравнение примет вид

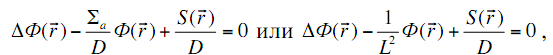(3.37)

где 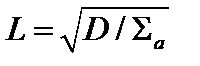– длина диффузии моноэнергетических нейтронов.

Уравнение (3.37) называют стационарным уравнением диффузии для неразмножающей среды. Если в среде возможно появление нейтронов деления, то в уравнении (3.23) добавляется слагаемое генерации нейтронов за счет деления ядер среды

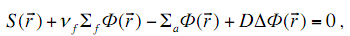
где n_f – число нейтронов деления при распаде одного ядра среды (урана-235).

Преобразуя, получаем стационарное уравнение диффузии для размножающей среды

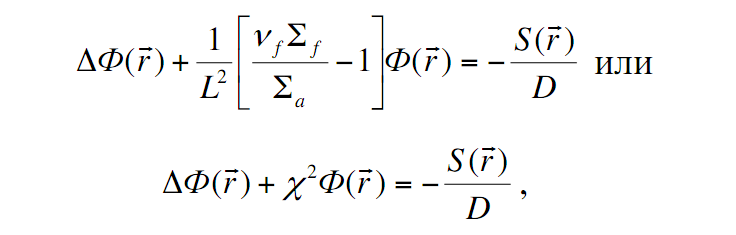
где 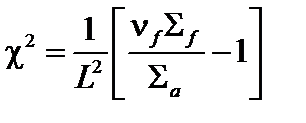– материальный параметр реактора (по англ. баклинг).

Если 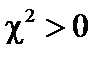, т.е. 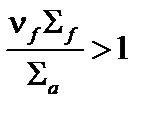– среда размножающая, поддерживающая цепную реакцию деления.

Если 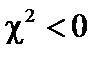, т.е. 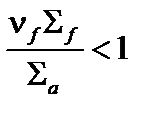– среда слабоделящаяся.

Если 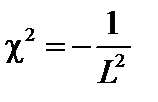, т.е. 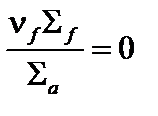– среда неделящаяся.

Время диффузии есть отношение свободного пробега и скорости теплового нейтрона до поглощения: t_д = l_a/υ = 1/(S_aυ). Скорость стандартных тепловых нейтронов (давление атмосферное, t=20°C) υ 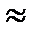2200 м/с. Для величин макросечений S_a применяемых в ядерных реакторах (ЯР) материалов время диффузии t_д = 10^-4–10^-5 с.