Оценка погрешности интерполяционного многочлена Лагранжа
Интерполяционный многочлен Лагранжа Ln(x) совпадает с функцией f(x) в узлах интерполяции х0, х1, х2, …, хn. Чтобы оценить степень приближения интерполяционного многочлена в точках, отличных от узлов интерполяции, надо сделать дополнительные предположения о поведении функции f(x), заданной таблично.
Будем считать, что функция f(x) дифференцируема n + 1 раз на отрезке [a,b]. Погрешность 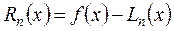 . Введем вспомогательную функцию
. Введем вспомогательную функцию 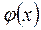 . Функция
. Функция 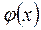 имеет n + 1 корень, т.е.
имеет n + 1 корень, т.е. 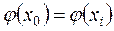 , т.к. в узлах интерполяции
, т.к. в узлах интерполяции 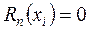
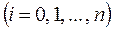 и один из сомножителей
и один из сомножителей 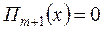 .
.
Подберем k таким образом, чтобы 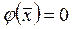 , т.е.
, т.е.
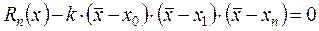 ,
,
тогда получим
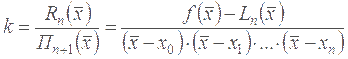 .
.
Определим численное значение коэффициента k. Для этого продифференцируем 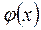 n + 1 раз. Так как
n + 1 раз. Так как 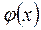 обращается в ноль на [a,b] в n + 2 точках: х0, х1, х2,…, хn, то на основании теоремы Ролля производная от
обращается в ноль на [a,b] в n + 2 точках: х0, х1, х2,…, хn, то на основании теоремы Ролля производная от 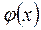 обращается в ноль , по крайней мере n + 1 раз на интервале [a, b].
обращается в ноль , по крайней мере n + 1 раз на интервале [a, b].
Применим снова теорему Ролля к функции 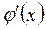 . Вторая производная
. Вторая производная 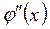 обращается в ноль не менее n раз на интервале (а, b). Продолжая этот процесс, придем к выводу, что производная (n + 1) порядка функции
обращается в ноль не менее n раз на интервале (а, b). Продолжая этот процесс, придем к выводу, что производная (n + 1) порядка функции 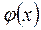 имеет хотя бы один корень, т.е.
имеет хотя бы один корень, т.е. 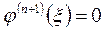 .
.
Тогда
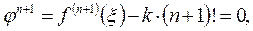

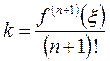 ,
,
но т.к.
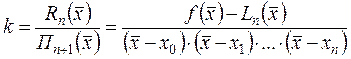 .
.
Получим
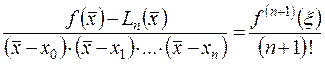 ,
,
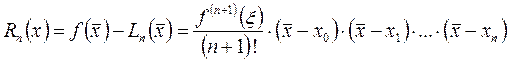 .
.
Полагая, что Mn+1 = max | f (n+1)(x)| получаем, оценку погрешности х Î [a, b] для интерполяционного многочлена Лагранжа
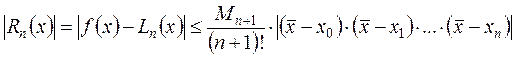 .
.
ЛЕКЦИЯ 7. КОНЕЧНЫЕ РАЗНОСТИ
Табулирование функций в большинстве случаев производится для равноотстоящих значений аргумента, т.е. 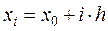 , где i = 0, 1, 2, …, n, а h – шаг интерполяции. Для вывода интерполяционных формул для равноотстоящих узлов интерполяции введем понятие «конечной разности».
, где i = 0, 1, 2, …, n, а h – шаг интерполяции. Для вывода интерполяционных формул для равноотстоящих узлов интерполяции введем понятие «конечной разности».
Назовем конечной разностью первого порядка разность между значениями функции в соседних узлах интерполяции
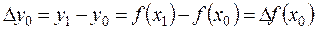 ,
,
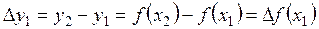 ,
,
… (7.1)
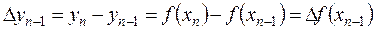 ,
,
где h = const, или в общем виде
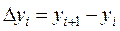 (7.2)
(7.2)
или
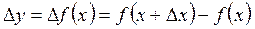 .
.
Из конечных разностей 1-го порядка можно образовать конечные разности 2-го порядка
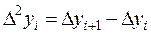 ;
; 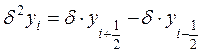 .
.
В общем виде конечная разность n-ого порядка записывается так:
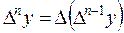 .
.
Дата добавления: 2021-09-07; просмотров: 578;











