Вектори кутової швидкості і кутового прискорення. Формула Ейлера

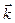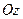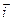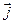Узагальнимо поняття про кутову швидкість тіла, що обертається навколо осі. Виберемо початок прямокутної декартової системи координат на осі обертання (рис.1.15) і вважатимемо, що вона незмінно зв’язана з тілом і обертається разом з ним. Орт лежить на нерухомій осі , орти і , зберігаючи модуль, змінюють напрям.

Визначимо швидкість довільної точки М тіла. На підставі (1.15)

.

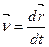Радіус-вектор 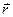розкладемо по ортах системи координат:

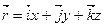. (а)

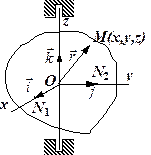
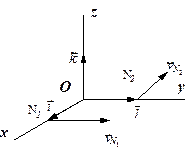
рис. 1.15	рис. 1.16

Координати точки 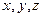і орт 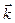не залежать від часу: орти 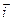і 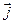є функції часу.Отже,

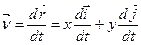. (в)

визначимо похідн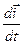і

і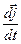

Вектор 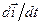можна розглядати як швидкість точки 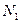, що викреслює годограф вектора 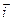. Модуль цієї швидкості

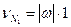(с)

Вектор 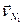напрямлений по дотичній до кола радіуса 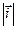, тобто перпендикулярно до осі 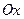і паралельно осі 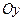(рис.1.16).

Згідно з цим дістанемо

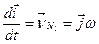. (d)

Якщо кутова швидкість 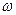додатня, то швидкість 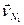збігається з ортом .

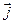Аналогічно знайдемо

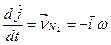. (е)

Згідно з (b), (d) і (е) швидкість точки М

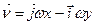. (f)

З курсу векторної алгебри відомі співвідношення

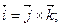
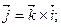
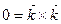. (g)

Підставивши (g) в (f), дістанемо

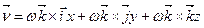. (h)

Винесемо за дужки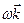

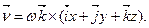(k)

Вектор 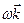називають вектором кутової швидкості :

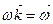. (1.45)

Як видно з (1.45), вектор 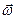напрямлений уздовж осі обертання у той бік, для якого обертальний рух має напрям ходу годинникової стрілки. Точка прикладання вектора 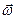на осі обертання довільна. Отже, 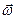ковзний вектор.

Тоді (k) набуває вигляду

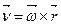. (1.46)

Цю формулу називають формулою Ейлера.

Вибравши осі координат, як показано на рис.1.16, знайдемо формули для проекцій лінійної швидкості на ці осі:

,

,

.

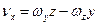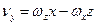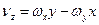Поняття вектора кутової швидкості і формулу Ейлера дістали, розглядаючи найпростіший обертальний рух тіла – обертання навколо нерухомої осі. Здобуті висновки буде поширено на більш загальні випадки руху твердого тіла.

Розглянемо вектор кутового прискорення 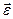. Кутове прискорення – це вектор, що характеризує бистроту зміни вектора кутової швидкості в часі. Тому

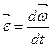. (1.47)

Очевидно, вектор 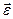напрямлений по дотичній до годографа вектора кутової швидкості. У розглянутому випадку годографом вектора 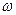є пряма, що збігається із віссю обертання. Отже, при обертанні тіла навколо нерухомої осі вектор кутового прискорення 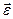напрямлений вздовж осі обертання.