Вероятность гипотез. Формула Байеса
Пусть событие А может наступить при условии появления одного из несовместных событий Н1, Н2, … , Нn, образующих полную группу. Поскольку заранее неизвестно, какое из этих событий наступит, их называют гипотезами. Вероятность события А определяется по формуле полной вероятности.
Допустим, что произведено испытание, в результате которого появилось событие А. Как изменились вероятности гипотез в связи с тем, что событие А уже наступило? Ответ на этот вопрос дает формула Байеса:
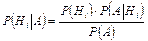 . .
| (2.13) |
Формула Байеса позволяет переоценить вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие А.
Пример 2.9. В условиях примера 2.8 оказалось, что взятая на контроль деталь оказалась нестандартной. Какова вероятность того, что она изготовлена на первом станке?
Решение. По условию необходимо переоценить вероятность гипотезы Н1, т.е. найти ее условную вероятность Р(Н1 |А) Ранее было получено: Р(Н1) = 40/100, Р(А/Н1) = 2/100, Р(А) = 0,031 = 310/10000. По формуле Байеса получаем:
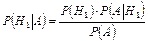 =
= 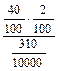 =
= 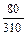 = 0,258. ◄
= 0,258. ◄
3. ПОВТОРНЫЕ НЕЗАВИСИМЫЕ ИСПЫТАНИЯ
На практике часто приходится сталкиваться с задачами, которые можно представить в виде многократных повторяющихся испытаний, проводимых при определенном комплексе условий. В этом случае интерес представляет вероятность числа m наступлений некоторого события А в n испытаниях. Например, необходимо определить вероятность определенного числа попаданий в мишень при нескольких выстрелах, вероятность некоторого числа бракованных изделий в данной партии и т.д.
Если вероятность наступления события А в каждом испытании не меняется в зависимости от исходов других, то такие испытания называются независимыми относительно события А. Если независимые повторные испытания проводятся при одном и том же комплексе условий, то вероятность наступления события А в каждом испытании одна и та же. Такая последовательность независимых испытаний получила название схемы Бернулли.
Формула Бернулли
Теорема. Если вероятность р наступления события А в каждом испытании постоянна, то вероятность Pn(m) того, что событие А наступит m раз в n независимых испытаниях, равна
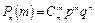 , ,
| (3.1) |
где q = 1 – p.
Пример 3.1. Вероятность поражения мишени в отдельном выстреле равна p = 0,8. Найти вероятности возможного числа попаданий при 5 выстрелах.
Решение. По условию р = 0,8, q = 1 – 0,8 = 0,2. По формуле Бернулли находим:
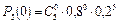 = 0,00032;
= 0,00032; 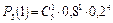 = 0,0064;
= 0,0064;
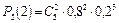 = 0,05120;
= 0,05120; 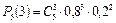 = 0,2048;
= 0,2048;
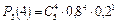 = 0,4096;
= 0,4096; 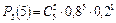 = 0,32768.
= 0,32768.
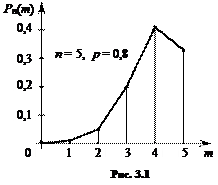 Полученные вероятности изобразим графически (рис. 3.1) точками с координатами (m; Pn(m)). Соединяя эти точки, получим многоугольник, или полигон, распределения вероятностей. ◄
Полученные вероятности изобразим графически (рис. 3.1) точками с координатами (m; Pn(m)). Соединяя эти точки, получим многоугольник, или полигон, распределения вероятностей. ◄
Рассматривая многоугольник распределения вероятностей, мы видим, что есть такое значение m (m0 = 4), которое обладает наибольшей вероятностью Pn(m).
Число m0 наступления события А в n независимых испытаниях называется наивероятнейшим, если вероятность осуществления этого события Pn(m0) по крайней мере не меньше вероятностей других событий Pn(m) при любом m.
Наивероятнейшее число наступления события А находится из двойного неравенства
| np – q ≤ m0 ≤ np + p. | (3.2) |
Отметим, что всегда существует целое число m0, удовлетворяющее этому неравенству. При этом, если np + p – целое число, то наивероятнейших чисел два: m0 = np + p и m0 = np – q.
Пример 3.2. В примере 3.1 мы нашли наивероятнейшее число попаданий m0=4, непосредственно вычисляя и сравнивая вероятности. Найдем наивероятнейшее число попаданий m0, используя неравенство (3.2):
5·0,8 – 0,2 ≤ m0 ≤ 5·0,8 + 0,8 → 3,8 ≤ m0 ≤ 4,8 → m0 = 4. ◄
Предположим, что мы хотим вычислить вероятность Pn(m) появления события А при большом числе испытаний n, например, P500(200). По формуле Бернулли
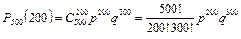 .
.
Ясно, что в этом случае непосредственное вычисление по формуле Бернулли технически сложно, тем более, если учесть, что сами p и q – числа дробные. Естественно возникает вопрос: нельзя ли вычислить интересующую нас вероятность, не прибегая к формуле Бернулли? Оказывается, можно. Существуют более простые приближенные формулы для вычисления при большом числе испытаний n. Такие формулы называют асимптотическими. Они определяются локальной теоремой Муавра-Лапласа, интегральной теоремой Лапласа, теоремой Пуассона.
Дата добавления: 2021-12-14; просмотров: 751;











