Вывод формулы Ньютона-Лейбница
Для нахождения определенного интеграла используют формулу Ньютона-Лейбница:
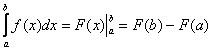 , где
, где 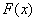 – первообразная функция для функции
– первообразная функция для функции 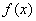 .
.
Докажем ее.
Рассмотрим тот же график 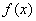 и познакомимся с функцией переменной площади
и познакомимся с функцией переменной площади 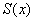 . Что это за функция? Зафиксируем произвольную точку
. Что это за функция? Зафиксируем произвольную точку 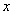 (левая красная точка), лежащую между точками «а» и «бэ»:
(левая красная точка), лежащую между точками «а» и «бэ»:
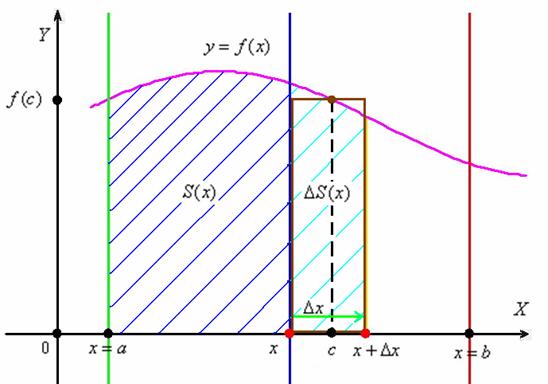
В данной точке функция 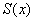 равна площади криволинейной трапеции, которая расположена между зелёной и синей линиями и заштрихована синим цветом. Мысленно начните уменьшать значение «икс» и сдвигать синюю прямую влево – площадь
равна площади криволинейной трапеции, которая расположена между зелёной и синей линиями и заштрихована синим цветом. Мысленно начните уменьшать значение «икс» и сдвигать синюю прямую влево – площадь 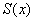 начнёт уменьшаться и, в конце концов, в точке
начнёт уменьшаться и, в конце концов, в точке 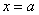 станет равной нулю:
станет равной нулю: 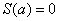 (прямые совпадут). Теперь возвращаемся на исходную позицию и сдвигаем синюю линию вправо – в этом случае площадь
(прямые совпадут). Теперь возвращаемся на исходную позицию и сдвигаем синюю линию вправо – в этом случае площадь 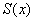 начнёт расти. И когда мы достигнем верхнего предела
начнёт расти. И когда мы достигнем верхнего предела 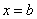 (синяя прямая «закроет» красную), площадь будет равна в точности площади всей криволинейной трапеции:
(синяя прямая «закроет» красную), площадь будет равна в точности площади всей криволинейной трапеции: 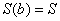 .
.
Таким образом, аргумент может изменяться в пределах 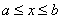 , при этом функция
, при этом функция 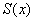 (площадь) будет возрастать от
(площадь) будет возрастать от 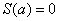 до
до 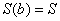 .
.
Докажем, что функция переменной площади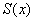 является первообразной функцией для функции
является первообразной функцией для функции 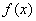 , то есть докажем, что
, то есть докажем, что 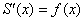 .
.
Вернёмся к нашей точке «икс» и зададим в ней приращение 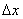 (зелёная стрелка). Для определённости полагаем, что
(зелёная стрелка). Для определённости полагаем, что 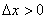 (случай
(случай 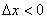 доказывается аналогично). Приращение аргумента
доказывается аналогично). Приращение аргумента 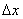 влечёт приращение функции
влечёт приращение функции 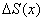 – геометрически это площадь криволинейной трапеции, которая заштрихована голубым цветом.
– геометрически это площадь криволинейной трапеции, которая заштрихована голубым цветом.
По так называемой теореме о среднем, на отрезке 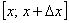 существует точка «цэ» – такая, что площадь коричневого прямоугольника равна площади голубой трапеции:
существует точка «цэ» – такая, что площадь коричневого прямоугольника равна площади голубой трапеции:
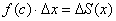
По определению производной, производная функции – это отношение приращения функции 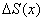 к приращению аргумента
к приращению аргумента 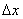 при
при 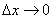 :
:
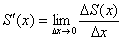 .
.
И, ввиду равенства 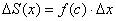 :
:
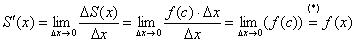
(*) Так как 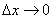 , то точка «цэ» бесконечно близко приближается к точке «икс», и, соответственно:
, то точка «цэ» бесконечно близко приближается к точке «икс», и, соответственно: 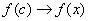
Вспомним, что в предыдущей главе мы доказали, что площадь криволинейной трапеции – есть предел интегральной суммы: 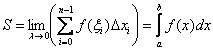 .
.
Но с другой стороны, 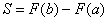 .
.
И из этих двух фактов следует лаконичная формула Ньютона-Лейбница:
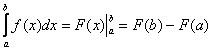 , где
, где 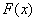 – первообразная функция для функции
– первообразная функция для функции 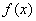 .
.


Дата добавления: 2020-06-09; просмотров: 900;











