АППРОКСИМАЦИЯ НЕКОТОРЫХ ТРАНСЦЕНДЕНТНЫХ ФУНКЦИЙ С ПОМОЩЬЮ РЯДОВ

Применение степенных рядов позволяет свести задачу вычисления значений функции к задаче вычисления полинома, т.е. к выполнению арифметических операций.

Разложение основных элементарных функций в степенные ряды известно из курса математического анализа. Для других функций это разложение может быть получено путем комбинации известных разложений или с помощью общей формулы Тейлора.

Напомним: функция f(x) называется аналитической в точке х₀, если для всех ½х – х₀½< r (r – радиус сходимости)

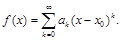
Очевидно, 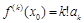(продифференцировав k раз).

Тогда 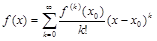(ряд Тейлора).

Таким образом, аналитическую функцию можно представить в виде бесконечного ряда. При конкретном вычислении возникает вопрос об ограничении ряда, т.е. о точности аппроксимации полиномом

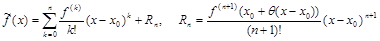
и об организации экономного суммирования.

Рассмотрим несколько конкретных примеров.

1°. Экспоненциальная функция.

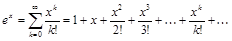
Этот ряд сходится при всех значениях х (½х½< ¥ ). Но при больших х может произойти потеря точности. Поэтому обычно поступают следующим образом. Представляют аргумент в виде :

х = [ x ] + q, где [ x ] – целая часть х , а 0 < q < 1.

Число е в целой степени находят многократным перемножением е само на себя, и ряд для экспоненты используют только для дробного показателя:

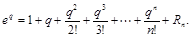
Для последовательного нахождения каждого члена ряда можно использовать рекуррентное соотношение

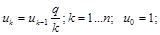
Пусть задана абсолютная погрешность суммирования данного ряда e. Когда остановить процесс вычисления суммы, то есть когда R_n < e ? Для этого оценим остаточный член.

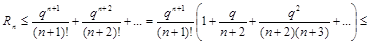
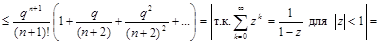
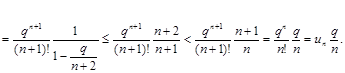
Таким образом, 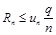, и процесс вычисления новых слагаемых можно прекращать, как только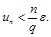

2°. Логарифмическая функция.

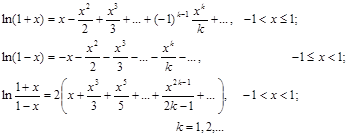
Рассмотрим последний ряд. Рекуррентное соотношение для нахождения очередного члена ряда имеет вид

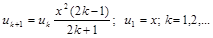
Можно ускорить процесс сходимости ряда, приблизив значение аргумента к нулю. Пусть необходимо вычислить ln t, где t – любое число. Представим t=2^mz, где 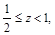m – целое число. Тогда ln t = mln 2 + ln z.

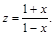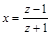Пусть Тогда , где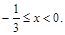

Следовательно, .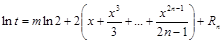

Оценим остаточный член.

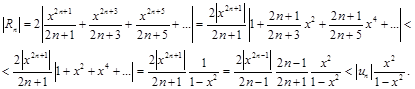Усиливая неравенство, получаем при х = –1/3 :

.

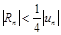Таким образом, 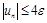– условие остановки суммирования.

3°. Тригонометрические функции.

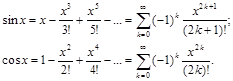
Рекуррентные соотношения для нахождения членов ряда имеют вид:

для sin x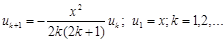

дляcos x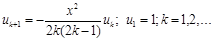

Так как ряды знакочередующиеся с монотонно убывающими членами, то для остаточного члена R_n справедлива оценка R_n £ e, поэтому процесс вычисления суммы прекращается при ½u_n½ £ e.

Эти ряды сходятся при всех х: ½x½< ¥. Но при этом подразумевается, что вычисление, например, синуса необходимо проводить с бесконечно большим количеством значащих цифр. Cтепенной ряд для синуса становится совершенно бесполезным при больших значениях аргумента и дает совершенно бессмысленные результаты.

Поэтому рекомендуется сводить аргумент к аргументу, лежащему в диапазоне0 £ х £ p/4 , используя формулы

sin(x+p/2+pn) = (–1)ⁿ cos x ; cos(x+p/2+pn) = (–1)ⁿ⁺¹ sin x.

Примечание 1. Улучшение скорости сходимости рядов.

Для увеличения скорости сходимости медленно сходящегося ряда необходимо из него вычесть (прибавить) ряд, сумма которого известна. Если скорость сходимости вновь полученного ряда вас не устраивает, то процесс можно повторить (метод Куммера).

Пример. 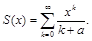Можно доказать, что этот ряд сходится при ½x½<1, хотя и медленно. Чем ближе х к нулю, тем сходимость быстрее.

Известно, что 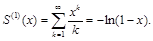(см. предыдущий пункт).

Тогда можно записать

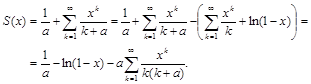
Последний ряд сходится быстрее, чем исходный.

Конец примечания 1.

Примечание 2. Об ошибках приближений с помощью рядов.

Характерной особенностью вычисления значений функции с помощью степенных рядов является тот факт, что ошибка (остаточный член) принимает максимальное значение при максимально возможном значении аргумента, например, в п.1° при ½q½~1 (рис.2.1)., в п.2° – при ½х½=1/3 .

Существует способ уменьшения ошибки в окрестности q=1, правда при этом ошибка увеличивается в других местах. Происходит ее перераспределение по всему интервалу. Это достигается при помощи полиномов Чебышева.

Конец примечания 2.