Аппроксимация на скользящем интервале.

При сплайн интерполяции ось Х разбивается на участки и проводится кусочная интерполяция. Так же можно поступать и при апроксимации, имея на каждом участке свой эталон, например, полином а+бХ+сХ²+... и оптимальным образом находить а,б,с, считая их оценками а^ б^ с^. Для нахождения оценок используем критерий минимума квадрата отклонения. В таблице 3 приведены формулы оценок а^,b^,c^.

Таблица 3

Аппроксимирующий полином	Оценки коэффициентов полинома	Остаточный квадрат
У=а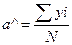
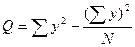
У=а+бх	;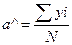
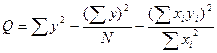
у=а+бх+сх2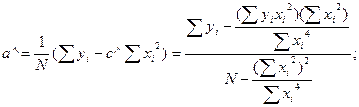

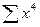Формулы таблицы приведены в центрированном виде, т.е. отсчет i идет от средней точки i=0 в плюс и минус i до значения N/2. Рассмотрение формул упрощается, если помнить, что коэффициенты типа и являются константами.

Если выделенный интервал перемещать по массиву исходных точек, то получаем эффект усредения на "скользящем" интервале. Нетрудно показать, что для случая апроксимирующего полинома Y=a+bX результат совпадает с эффектом пропускания массива сигнала черех фильтр с прямоугольным откликрм, база этого отклика равна величине скользящего интервала.