Аппроксимация модели по переходной характеристике

Аппроксимация экспериментальной переходной характеристики 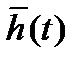заключается в выборе аналитического выражения и вычислении коэффициентов математической модели объекта. Существуют несколько способов аппроксимации, отличающихся выбранной математической моделью и критерием приближения переходной характеристики реального объекта 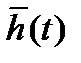и модели h_a(t) [14].

Реальные переходные процессы в АСУ достаточно точно могут быть описаны как линейными дифференциальными уравнения высокого порядка, так и линейными уравнениями второго порядка с запаздыванием (принцип акад. А. Ю. Ишлинского). Если кривая переходной характеристики h(t), начиная с момента времени 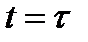, незначительно отличается от экспоненты, а до момента времени 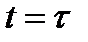ординаты графика достаточно малы (рис. 22), то соответствующее приближенное значение передаточной функции объекта можно записать в виде:

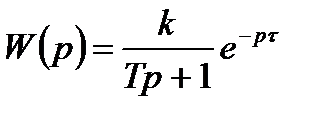. (8)

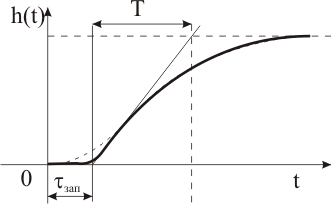
Рисунок 22 – Экспериментальная и аппроксимированная переходные характеристики

В выражении (8) параметры Т и t определяются по кривой разгона с применением того или иного метода обработки экспериментальных данных.

При наличии большого числа последовательно включенных апериодических звеньев первого порядка с единичным коэффициентом усиления и малым значением постоянной времени 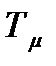их можно заменить на звено с запаздыванием:

.

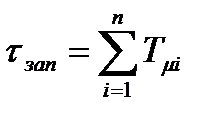Рассмотрим доказательство сформулированного утверждения. Пусть систем содержит n последовательно включенных одинаковых инерционных звеньев первого порядка, значения параметров которых удовлетворяют условиям, записанным выше, т.е. 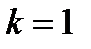, 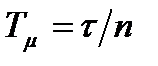. Эквивалентная передаточная функция будет равна:

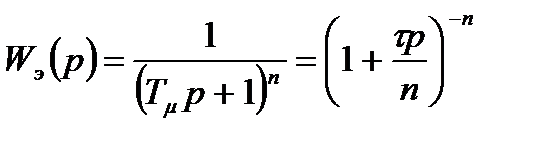. (9)

Возьмем предел левой части выражения (3) при :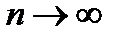

.

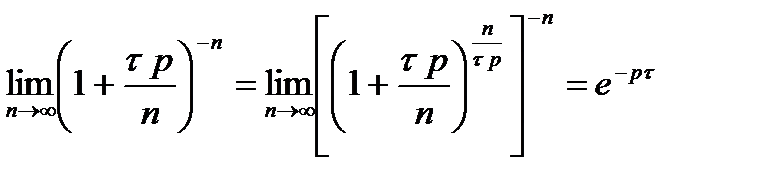Таким образом, передаточную функцию с n последовательно включенными апериодическими звеньями при большом значении n ( 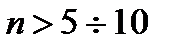), можно аппроксимировать звеном запаздывания с параметром:

.

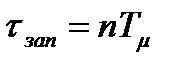Наличие в структурной схеме АСУ звена с запаздыванием затрудняет решение и анализ трансцендентного уравнения характеристического полинома. В связи с этим передаточную функцию запаздывающего звена иногда представляют в виде ряда Пада, учитывая только первые два его члена:

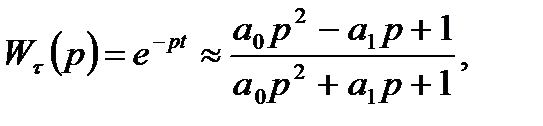(10)

где ; .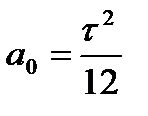

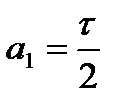Полученная передаточная функция (10) имеет «правые» корни числителя, следовательно, данное звено, как и типовое звено с запаздыванием не является минимально-фазовым.