Общее уравнение динамики

В соответствии с принципом Даламбера для любой механической системы

.

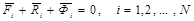Применяем принцип возможных перемещений. Умножая каждое из уравнений (4.8) на возможное перемещение точки 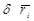(рис. 4.4) и суммируя по всем точкам системы, получим

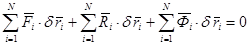(4.9)

Рисунок 4.4

Для систем с идеальными связями 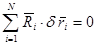и выражение (4.9) примет вид

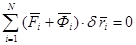(4.10)

Выражение (4.10) - одна из форм записи общего уравнения динамики. Учитывая, что 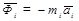, получим другую форму записи общего уравнения динамики

(4.11)

Таким образом, согласно общему уравнению динамики, в любой момент движения системы с идеальными связями сумма элементарных работ всех активных сил и сил инерции точек системы равна нулю на любом возможном перемещении системы, допускаемом связями.

В декартовой системе координат получим

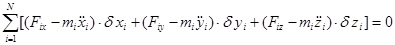(4.12)

Выражение (4.12) называют общим уравнением динамики в аналитической форме.

СПИСОК ЛИТЕРАТУРЫ

1. Тарг С.М. Краткий курс теоретической механики: Учебник для втузов / С.М Тарг – М.: Высшая школа, 2004г. – 416с.

2. Маркеев А.П. Теоретическая механика: Учебник для университетов. / А.П Маркеев - 3-е изд. — М.: Ижевск: РХД, 2007.— 592с.

3. Богачева С.Ю. Статика. Плоская система сил: Методические указания для самостоятельной работы студентов / С.Ю Богачева. – М.: 2008. – 32 с.

4. Абрамов В.Ф., Богачева С.Ю. Определение кинематических параметров в плоскопараллельном движении твердого тела: Методические указания для самостоятельной работы студентов / В.Ф. Абрамов, С.Ю. Богачева – М.:МГУДТ, 2015. - 32с.