Решение второй задачи динамики в декартовых координатах

Дано: 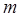, 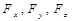. Определить .

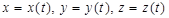Проецируя уравнение (3.4) на координатные оси получим систему трех скалярных уравнений второго порядка

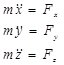(3.5)

В этих уравнениях проекции силы на координатные оси в общем случае являются функциями времени, координат и скоростей точки, то есть

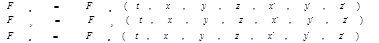(3.6)

Решение системы уравнений (3.5) проводится с учетом функциональных зависимостей (3.6). Общее решение системы можно представить в виде

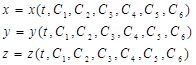
Произвольные постоянные 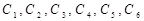определяются из начальных условий. Подставляя в начальные условия общее решение, записанное для 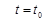получим шесть уравнений для определения шести произвольных постоянных

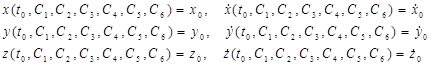(3.7)

Определяем произвольные постоянные из уравнений (3.7) и подставляем их в общее решение. Получаем частное решение, то есть решение основной задачи динамики.

3.2. Геометрия масс

Центром масс системы называется геометрическая точка С, радиус вектор которой определяется выражением

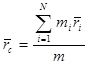(3.8)

где 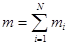- масса системы.

Моменты инерции относительно центра и оси. Момент инерции механической системы относительно центра О называется сумма произведений масс точек системы на квадраты их расстояний до центра О (рисунок 3.2) .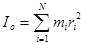

В случае сплошного тела сумма переходит в интеграл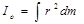

где 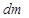- масса элементарной частицы тела, принимаемой в пределе за точку,

r – ее расстояние до точки О.

Моментом инерции системы материальных точек относительно оси u называется сумма произведений масс этих точек на квадрат их расстояний до оси u

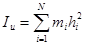
В частном случае сплошного тела сумму следует заменить интегралом

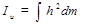Рисунок 3.2.