Теорема об изменении количества движения системы

К каждой точке системы приложим равнодействующие внешних и внутренних сил (рисунок 3.8). Для каждой точке системы можно применить теорему об изменении количества движения, например в форме (3.20)

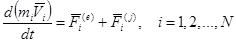
Суммируя по всем точкам системы и учитывая, что сумма производных равна производной от суммы, получим

.

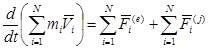По определению количества движения системы и свойству внутренних и внешних сил

,

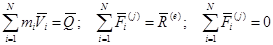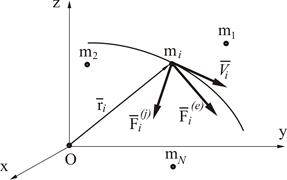
Рисунок 3.8

поэтому полученное соотношение можно представить в виде

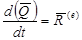(3.23)

Выражение (3.23) является теоремой об изменении количества движения системы в дифференциальной форме: производная по времени количества движения системы равна главному вектору внешних сил. Если умножить обе части выражения на dt, то получим другую форму этой теоремы

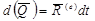(3.24)

то есть дифференциал количества движения системы равен элементарному импульсу главного вектора внешних сил. Интегрируя обе части в пределах от t₁ до t₂ , получим интегральную форму теоремы

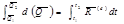или

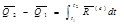(3.25)

где 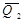- количество движения системы в конечный момент времени t₂,

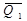- количество движения системы в начальный момент времени t₁.

Приращение количества движения системы за некоторое время равно импульсу главного вектора внешних сил за то же время.

3.3.4. Момент количества движения материальной точки. Кинетический момент системы

Для материальной точки массой m, движущейся со скоростью 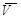,момент количества движения относительно центра О равен.

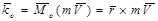(3.26)

Момент количества движения 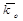приложен к точке О, относительно которой он вычисляется (рис. 3.9).

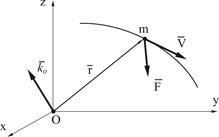
Рисунок 3.9

Моментом количества движения точки относительно оси z называют алгебраический момент проекции количества движения точки 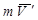на плоскость П (рис. 3.10), перпендикулярную оси z, относительно точки пересечения оси с этой плоскостью .

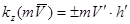Для механической системы моментом количества движения (кинетическим моментом) относительно какой-либо точки О называют векторную сумму моментов количества движения точек этой системы, взятых относительно точки О

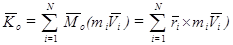(3.27)

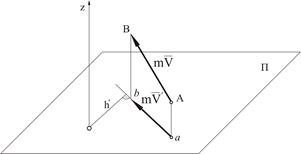
Рисунок 3.10

Кинетический момент системы 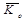приложен к точке О, относительно которой он вычисляется.

Кинетический момент механической системы относительно оси z равен алгебраической сумме моментов количества движения всех точек системы относительно той же оси

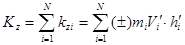(3.28)