Теорема об изменении кинетической энергии материальной системы

К каждой точке системы приложим равнодействующие внешних и внутренних сил (рис. 3.5). Для каждой точке системы можно применить теорему об изменениикинетической энергии, например в форме (3.48)

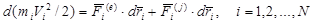
Суммируя правые и левые части этих соотношений по всем точкам системы и вынося знак дифференциала за знак суммы, получаем

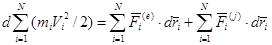
или

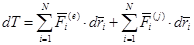(3.50)

Дифференциал кинетической энергии системы равен сумме элементарных работ всех внешних и внутренних сил, действующих на систему. Интегрируя обе части (3.50) в пределах от t₁ до t₂ и вынося знак суммы за знак интеграла, получим

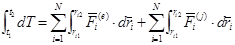
или 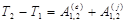(3.51)

где 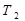- кинетическая энергии системы в конечный момент времени t₂,

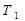- кинетическая энергии системы в начальный момент времени t₁,

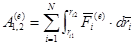- сумма работ внешних сил и

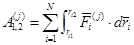- сумма работ внутренних сил на перемещениях точек системы из начального положения в конечное.

Пример определения кинетической энергии системы. Для заданного положения механизма (рисунок 3.17) составить уравнение для определения кинетической энергии, пренебрегая массой 4-го звена.

Рисунок 3.17

Кинетическая энергия первого и пятого звена, вращающихся вокруг неподвижных осей, определяется ,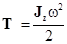

где 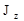- момент инерции тела относительно оси вращения,

w – угловая скорость вращения тела.

Кинетическая энергия 2 тела, совершающего плоскопараллельное движение,

,

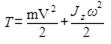где 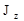- момент инерции тела относительно оси z, проходящей через центр тяжести,

w – угловая скорость вращения тела,

V – скорость центра тяжести тела.

Кинетическая энергия 3 тела, движущегося поступательно ,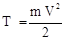

где V – скорость точки твердого тела.

Получим уравнение для определения кинетической энергии

.

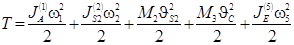4. элементы Аналитической механики