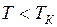I.3.1 УРАВНЕНИЕ ВАН-ДЕР-ВААЛЬСА

Газом Ван–дер–Ваальса называется такая модель реального газа, в которой молекулы рассматриваются как абсолютно твёрдые шарики с диаметром d, между которыми действуют силы взаимного притяжения. Конечные размеры шариков означают, что принимаются во внимание и силы отталкивания между молекулами реального газа.

Уравнение состояния реальных газов получается из уравнения состояния идеального газа (I.13), после небольшого видоизменения, а именно, в случае реальных газов давление следует увеличить на величину так называемого внутреннего давления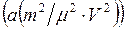, которое возникает вследствие межмолекулярного взаимодействия и пропорционально квадрату плотности газа. Объем следует уменьшить на величину 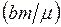собственного объема молекул– того минимального объема, который могут занимать молекулы данной массы газа. Собственный объем молекул приблизительно в четыре раза больше реального объема молекул.

В результате получаем уравнение Ван–дер–Ваальса(уравнение состояния реальных газов)

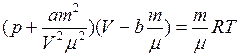, (I.73)

где 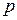– давление газа; 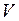– объем газа; 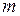– масса газа; 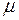– молярная масса газа; 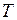– температура; 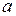, 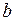– (коэффициенты пропорциональности) постоянные Ван–дер–Ваальса, имеющие для разных газов различные значения, определяемые экспериментально (значения некоторых из них приведены в приложении Б., таблица Б.5).

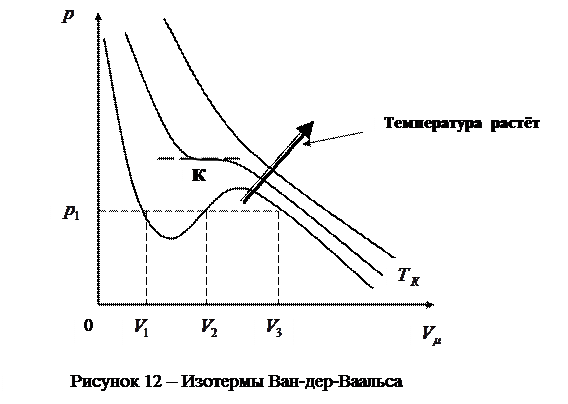
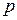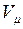Для исследования поведения реального газа рассмотрим изотермы Ван– дер– Ваальса – кривые зависимости от (молярный объём) (рис.12) при заданных 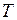, определяемые уравнением Ван – дер – Ваальса для моля газа (ещё одна форма записи)

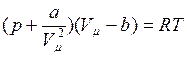. (I.74)

Эти кривые рассматриваются для трёх различных температур. При высоких температурах 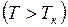изотерма реального газа отличается от изотермы идеального газа только некоторым искажением её формы, оставаясь монотонно спадающей кривой. При некоторой температуре 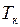на изотерме имеется лишь одна точка перегиба К. Эта изотерма называется критической, соответствующая ей температура 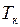– критической температурой. Критическая изотерма имеет лишь одну точку перегиба К, называемую критической точкой; в этой точке касательная к ней параллельна оси абсцисс. Соответствующие этой точке объём 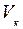и давление 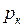называются также критическими. Состояние с критическими параметрами 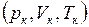называется критическим состоянием. При низких температурах 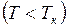изотермы имеют волнообразный участок, сначала монотонно опускаясь вниз, затем монотонно поднимаясь вверх и снова монотонно опускаясь.

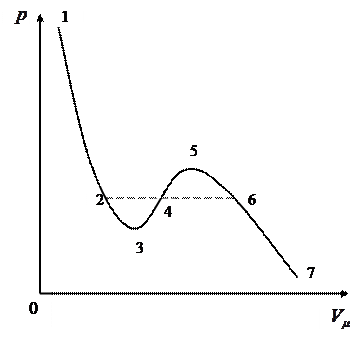
Выделим и проанализируем изотерму Ван–дер–Ваальса для случая 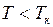(рис.13).

Рисунок 13 – Изотерма Ван-дер-Ваальса при

Рассматривая различные участки данной изотермы, видим, что на участках (1– 3) и (5– 7) при уменьшении объёма давление возрастает. На участке (3 – 5) сжатие вещества приводит к уменьшению давления. Наличие этого участка означает, что при постепенном изменении объёма вещество не может оставаться всё время в виде однородной среды; в некоторый момент должно наступить скачкообразное изменение состояния и распад вещества на две фазы (в термодинамике фазой называется совокупность всех частей системы, обладающих одинаковым химическим составом и находящихся в одинаковом состоянии). Таким образом, истинная изотерма будет иметь вид ломаной линии (7– 6– 2– 1). Часть (7– 6) отвечает газообразному состоянию, а часть (2 – 1) – жидкому. В состояниях, соответствующих горизонтальному участку изотермы (6 – 2), наблюдается равновесие жидкой и газообразной фаз вещества. Вещество в газообразном состоянии при температуре ниже критической называется паром, а пар, находящийся в равновесии со своей жидкостью, называется насыщенным.