I.4.2 ОСНОВНОЙ ЗАКОН ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

Твёрдое тело, вращающееся вокруг некоторых осей, проходящих через центр масс, если оно освобождено от внешних воздействий, сохраняет вращение неопределённо долго. (Это заключение аналогично первому закону Ньютона для поступательного движения).

Возникновение вращения твёрдого тела всегда вызывается действием внешних сил, приложенных к отдельным точкам тела. При этом неизбежно возникновение деформаций и появление внутренних сил, обеспечивающих в случае твёрдого тела практическое сохранение его формы. При прекращении действия внешних сил вращение сохраняется: внутренние силы не могут ни вызвать, ни уничтожить вращение твёрдого тела.

Результатом действия внешней силы на тело, имеющее неподвижную ось вращения, является ускоренное вращательное движение тела. (Это заключение аналогично второму закону Ньютона для поступательного движения).

Основной закон динамики вращательного движения: в инерциальной системе отсчёта угловое ускорение 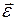, приобретаемое телом, вращающимся относительно неподвижной оси, пропорционально суммарному моменту всех внешних сил 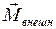, действующих на тело, и обратно пропорционально моменту инерции тела 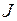относительно данной оси:

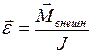. (I.109)

Можно дать и более простую формулировку основному закону динамики вращательного движения (его ещё называют вторым законом Ньютона для вращательного движения): вращающий момент равен произведению момента инерции на угловое ускорение:

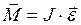. (I.110)

Моментом импульса 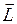(моментом количества движения, угловым моментом) тела называется произведение его момента инерции 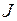на угловую скорость :

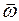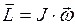. (I.111)

Момент импульса – векторная величина. Его направление совпадает с направлением вектора угловой скорости.

Изменение момента импульса определяется следующим образом:

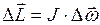. (I.112)

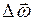Изменение момента импульса (при неизменном моменте инерции тела) может произойти, только вследствие изменения угловой скорости и всегда обусловлено действием момента силы .

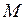Согласно формуле 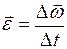, а также формулам (I.110) и (I.112) изменение момента импульса можно представить в виде:

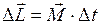. (I.113)

Произведение 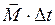в формуле (I.113) называется импульсом момента силы или движущим моментом. Он равен изменению момента импульса.

Формула (I.113) справедлива при условии, что момент силы не меняется с течением времени 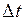. Если же момент силы зависит от времени, т.е. 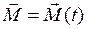, то

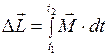. (I.114)

Формула (I.114) показывает, что: изменение момента импульса равно интегралу по времени от момента силы. Кроме того, если эту формулу представить в виде: 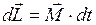, то из неё будет следовать определение момента силы: мгновенный момент силы представляет собой первую производную момента импульса по времени,

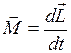. (I.115)

Выражение (I.115) является ещё одной формой основного уравнения (закона) динамики вращательного движения твёрдого тела относительно неподвижной оси: производная момента импульса твёрдого тела относительно оси равна моменту сил относительно той же оси.

В замкнутой системе момент внешних сил 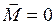и 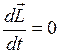, следовательно:

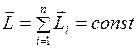. (I.116)

Формула (I.116) представляет собой закон сохранения момента импульса: векторная сумма всех моментов импульса относительно любой оси для замкнутой системы остается постоянной в случае равновесия системы. В соответствии с этим, момент импульса замкнутой системы относительно любой неподвижной точки не изменяется со временем Закон сохранения момента импульса – фундаментальный закон природы.

Обратите внимание: полный момент импульса системы равен векторной сумме моментов импульса отдельных частей системы.