I.6.3 ДВИЖЕНИЕ ЖИДКОСТЕЙ И ГАЗОВ. УРАВНЕНИЕ БЕРНУЛЛИ

Движение (течение) жидкости называется стационарным(установившимся), если в заданных точках пространства скорость жидкости не зависит от времени. При этом в разных точках пространства скорости жидкости могут быть неодинаковыми.

Если в фиксированных точках пространства скорость жидкости с течением времени изменяется, движение называется нестационарным(неустановившимся).

Наблюдается два вида течения жидкости (или газа).

Движение, при котором наблюдается правильное перемещение слоёв жидкости приблизительно параллельными струями, без перемешивания называется ламинарным движением (слоистым). Ламинарное течение может быть как стационарным, так и нестационарным.

Ламинарное движение – движение с трением, сохраняющее слоистость.

Можно сказать и так: течение жидкостей при наличии внутреннего трения, но не сопровождающееся образованием вихрей, называется ламинарным. Если в ламинарный поток ввести подкрашенную струйку, то она сохраняется, не размываясь, на всей длине потока, так как частицы жидкости в ламинарном потоке не переходят из одного слоя в другой.

При увеличении скорости или поперечных размеров потока характер течения существенным образом изменяется. Возникает энергичное перемешивание жидкости. Такое течение называется турбулентным. При турбулентном течении скорость частиц в каждом данном месте всё время изменяется беспорядочным образом – течение нестационарно. Если в турбулентный поток ввести окрашенную струйку, то уже на небольшом расстоянии от места её введения окрашенная жидкость равномерно распределяется по всему сечению потока.

Линия, касательная к которой в данной точке совпадает по направлению со скоростью жидкости в этой точке в данный момент времени, называется линией тока. При стационарном течении жидкости линии тока совпадают с траекториями частиц жидкости.

Трубкой тока называется поверхность, образованная линиями тока, проведёнными через все точки малого замкнутого контура, выделенного внутри жидкости. Жидкость, протекающую по всей совокупности трубок тока, называют потоком.

При стационарном течении масса жидкости, проходящей через любое поперечное сечение трубки тока за единицу времени, остаётся неизменной. Жидкость не скапливается в отдельных частях трубки тока, не образует пустот и не переходит в соседние трубки тока. Это позволяет написать уравнение неразрывностидля стационарного течения жидкости:

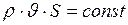, (I.145)

где 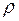- плотность жидкости; 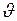- модуль скорости жидкости в произвольном поперечном сечении трубки тока площадью .

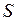Если жидкость несжимаема, то плотность во всех сечениях трубки тока одна и та же 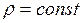и уравнение неразрывности принимает вид .

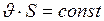Следствием закона сохранения механической энергии для стационарного течения несжимаемой невязкой жидкости по трубке тока является уравнение Бернулли(уравнение гидродинамики, полученное швейцарским математиком Даниилом Бернулли (1738 г)):

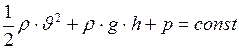, (I.146)

где 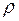- плотность жидкости;

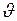- модуль скорости течения жидкости в сечении трубки тока, находящемся на высоте 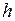от условно выбранного уровня;

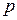- давление в том же сечении трубки тока, вызванное силами упругости жидкости.

Для выяснения физического смысла всех членов, входящих в формулу (I.146), умножим их на объём .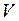

Физическое значение входящих в формулу (I.146) величин:

q 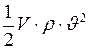- это кинетическая энергия жидкости в единице объёма, двигающейся со скоростью ;

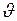q 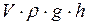- это потенциальная энергия жидкости в единице объёма, поднятой на высоту ;

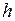q 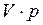- это потенциальная энергия жидкости, измеряемая работой, которую произвела бы жидкость под действием давления 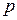, перейдя из положения 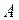в положение 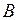(рис.41), отодвинув стенку 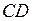в положение .

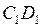Следовательно, уравнение Бернулли устанавливает, что при стационарном движении жидкости сумма кинетической энергии, потенциальной энергии тяжести и потенциальной энергии давления есть величина постоянная для всякого сечения.

Для горизонтальной трубки тока ( 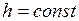) уравнение Бернулли упрощается:

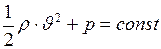. (I.147)

В этом уравнении:

q 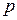- статическое давление, оно обусловлено потенциальной энергией жидкости, находящейся под давлением;

q 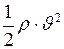- динамическое давление (давление напора), обусловлено кинетической энергией движущейся жидкости;

q 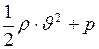- полным давлением .

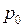Из уравнения (I.147) следует, что в тех сечениях трубки тока, где скорость жидкости больше, статическое давление меньше, а в тех сечениях, где скорость жидкости уменьшается, статическое давление возрастает.

Уравнение (I.147) представляет собой закон Бернулли: в стационарном потоке сумма статического и динамического давлений остаётся постоянной. Эта сумма соответствует гидростатическому давлению в покоящейся жидкости.

Закон истечения жидкости из сосуда – закон Торичелли (1643г.): скорость истечения жидкости из отверстия равна по величине скорости свободного падения с высоты, равной высоте столба жидкости.

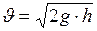, (I.148)

где 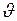- скорость истечения жидкости; 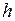- высота столба жидкости;

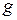- ускорение свободного падения.