Принцип возможных перемещений

Принцип возможных перемещений или принцип Лагранжа относится к системам, находящимся в равновесии и дает уравнения равновесия системы со стационарными, идеальными удерживающими связями.

Рассмотрим систему материальных точек (рис. 4.2).

Рисунок 4.2

Поскольку система находится в равновесии, то для каждой ее точки можно записать уравнение равновесия

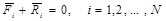(4.3)

где 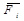- равнодействующая активных сил, приложенных к i-ой точке,

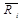- равнодействующая реакции связей, приложенных к i-ой точке.

Дадим системе возможное перемещение. Умножая обе части равенства (4.3) на возможное перемещение точки 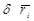и суммируя по всем точкам системы получим

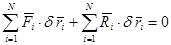(4.4)

Так как связи идеальные, то 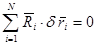и выражение (4.4) примет вид

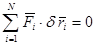(4.5)

Для равновесия системы со стационарными, идеальными удерживающими связями необходимо и достаточно, чтобы сумма работ активных сил системы на любом возможном перемещении равнялась нулю.

Принцип Даламбера

Уравнение движения материальной точки массой m (рисунок 4.3) под действием приложенных активных сил и реакций связей имеет вид

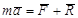(4.6)

где 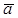- ускорение точки,

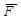- равнодействующая активных сил,

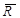- равнодействующая реакции связей

Силой инерции материальной точки называется величина

.

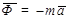Рисунок 4.3

С использованием этой величины уравнение (4.6) можно записать в виде

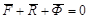(4.7)

Уравнение (4.7) выражает принцип Даламбера для материальной точки: При движении материальной точки активные силы, реакции связей вместе с силой инерции точки образуют равновесную систему сил.

Рассмотрим систему N материальных точек. К каждой точке системы приложены равнодействующая активных сил и равнодействующая реакций связей. Применяя принцип Даламбера к каждой точке системы, получим

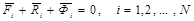(4.8)

где 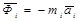- сила инерции для к i-ой точки.

N векторных уравнений (4.8) выражают принцип Даламбера для системы: при движении механической системы активная сила и реакция связей вместе с силой инерции составляют равновесную систему сил для каждой точки системы.