Теорема об изменении момента количества движения точки

Для материальной точки основной закон динамики можно представить в виде

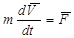
Умножая обе части этого соотношения слева векторно на радиус-вектор (рис. 3.9), получаем

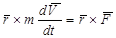(3.32)

В правой части этой формулы имеем момент силы относительно точки О. Преобразуем левую часть, применив формулу производной векторного произведения

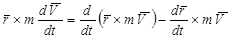
Но 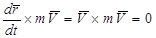как векторное произведение параллельных векторов. После этого получаем

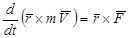(3.33)

или

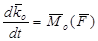(3.34)

Первая производная по времени момента количества движения точки относительно какого-либо центра равна моменту силы относительно того же центра.

Пример вычисления кинетического момента системы. Вычислить кинетический момент относительно точки О системы, состоящей из цилиндрического вала массой М = 20 кг и радиусом R = 0.5м и спускающегося груза массой m = 60 кг (рисунок 3.12). Вал вращается вокруг оси Oz с угловой скоростью ω = 10 с^-1.

Рисунок 3.12

; ;

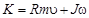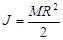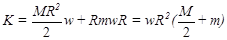
При заданных входных данных кинетический момент системы

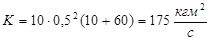
Теорема об изменении кинетического момента системы. К каждой точке системы приложим равнодействующие внешних и внутренних сил. Для каждой точке системы можно применить теорему об изменении момента количества движения, например в форме (3.33)

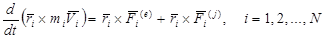
Суммируя по всем точкам системы и учитывая, что сумма производных равна производной от суммы, получим

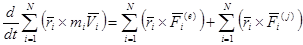
По определению кинетического момента системы и свойству внешних и внутренних сил

,

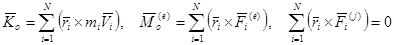поэтому полученное соотношение можно представить в виде

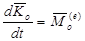(3.35)

Первая производная по времени кинетического момента системы относительно какой-либо точки равна главному моменту внешних сил, действующих на систему, относительно той же точки.

3.3.5. Работа силы

1) Элементарная работа силы равна скалярному произведению силы на дифференциал радиус вектора точки приложения силы (рис. 3.13)

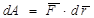(3.36)

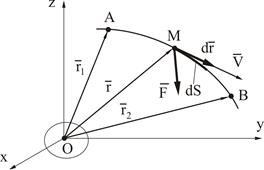
Рисунок 3.13

Выражение (3.36) можно записать также в следующих эквивалентных формах

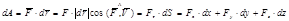(3.37)

где 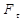- проекция силы на направление скорости точки приложения силы.

2) Работа силы на конечном перемещении

Интегрируя элементарную работу силы, получим следующие выражения для работы силы на конечном перемещении из точки А в точку В

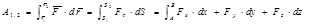(3.38)

3) Работа постоянной силы

Если сила постоянна, то из (3.38) следует

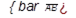(3.39)

Работа постоянной силы не зависит от формы траектории, а зависит только от вектора перемещения точки приложения силы .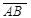

4) Работа силы веса

Для силы веса (рис. 3.14) и из (3.39) получим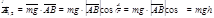

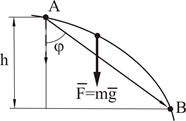
Рисунок 3.14

Если движение происходит из точки В в точку А, то

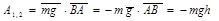
В общем случае

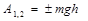(3.40)

Знак «+» соответствует движению точки приложения силы «вниз», знак «-» - вверх.

4) Работа силы упругости

Пусть ось пружины направлена по оси x (рис.3.15), а конец пружины перемещается из точки 1 в точку 2, тогда из (3.38) получим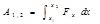

Если жесткость пружины равна с, то 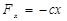, тогда

А 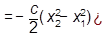(3.41)

Если конец пружины перемещается из точки 0 в точку 1, то в этом выражении заменяем 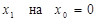, , 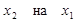тогда работа силы упругости примет вид

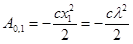(3.42)

где 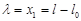- удлинение пружины.

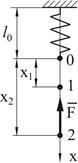
Рисунок 3.15

5) Работа силы приложенной к вращающемуся телу. Работа момента.

На рис. 3.16 показано вращающееся тело, к которому приложена произвольная сила . При вращении точка приложения этой силы движется по окружности.

Рисунок 3.16

В соответствии с (33) элементарная работа силы 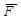равна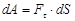

где 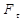- проекция силы на направление касательной к окружности. Учитывая, что 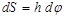получим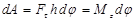

где 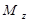- момент силы 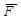относительно оси z. Полная работа

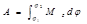(3.43)

где 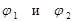- начальное и конечное значения угла поворота тела.

В частном случае постоянного момента

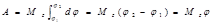(3.44)

где 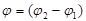- угол поворота тела, на котором вычисляют работу силы.

3.3.6. Кинетическая энергия точки и системы

Кинетической энергией материальной точки называют половину произведения массы точки на квадрат ее скорости

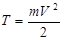
Кинетической энергией системы называют сумму кинетических энергий всех точек механической системы

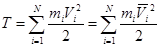(3.45)