Условие статической определимости кинематической цепи

Число неизвестных, определяемых из какой-либо системы уравнений, должно совпадать с числом уравнений. Для n звеньев, на которые действует пространственная система сил общего вида, можно составить 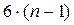уравнений статики (кинетостатики) приравняв нулю суммы проекций сил на координатные оси и суммы моментов сил относительно этих осей. Число неизвестных, подлежащих определению из этих уравнений, для каждой кинематической пары совпадает с числом связей, так как невозможность движения вдоль оси дает реакцию в виде силы, а невозможность вращения вокруг оси – в виде пары сил.

Условие статической определимости пространственной кинематической цепи имеет вид:

,

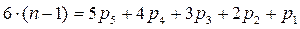Где 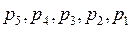- число одно-, двух-, трех-, четырех-, пятиподвижных пар. Это условие совпадает с условием равенства нулю числа степеней свободы, то есть статически определимыми являются структурные группы Ассура.

Для плоских кинематических цепей число уравнений статики равно 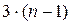. Условие статической определимости для плоской кинематической цепи имеет вид:

,

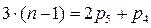так как в плоском механизме для каждой одноподвижной пары число неизвестных равно двум: величина силы и ее направление или точка приложения (координата), а для высшей двухподвижной пары в плоском механизме число неизвестных равно одному: модуль реакции, так как направление этой реакции и точка приложения реакции известны (рис. 30).

Однако это условие справедливо только для плоской системы сил, действующей на звенья механизма. При пространственном расположении сил число уравнений статики и число неизвестных составляющих реакций должно удовлетворять условию статической определимости пространственной кинематической цепи.

Наличие избыточных связей увеличивает число неизвестных составляющих реакций, и для их определения дополнительно к уравнениям статики должны быть составлены уравнения деформаций.