Активное сопротивление, индуктивность и емкость в цепи переменного тока.

Изме­нения силы тока, напряжения и э. д. с. в цепи переменного тока происходят с одинаковой частотой, но фазы этих изменений, вооб­ще говоря, различны. Поэтому если начальную фазу силы тока ус­ловно принять за нуль, то начальная фаза напряжения будет иметь некоторое значение φ. При таком условии мгновенные значения силы тока и нап­ряжения и будут выражаться следующими формулами:

i = I_msinωt

u = U_msin(ωt + φ)

a) Активное сопротивление в цепи переменного тока. Сопротивление цепи, которое обу­словливает безвозвратные потери элект­рической энергии на тепловое действие тока, называют активным. Это сопротив­ление для тока низкой частоты можно счи­тать равным сопротивлению R этого же проводника постоянному току.

В цепи переменного тока, имеющей только активное сопротивле­ние, например, в лампах накаливания, нагревательных приборах и т. п., сдвиг фаз между напряжением и током равен нулю, т. е. φ = 0. Это означает, что ток и напряжение в такой цепи изменяются в оди­наковых фазах, а электрическая энергия полностью расходуется на тепловое действие тока.

Будем счи­тать, что напряжение на зажимах цепи меняется по гармоническому закону: и = U_т cos ωt.

Как и в случае постоянного тока, мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения. Поэтому для нахождения мгновенного значе­ния силы тока можно применить закон Ома:

В проводнике с активным сопротивлением колебания силы тока совпадают

по фазе с колебаниями напряже­ния.

b) Катушка индуктивности в цепи переменного тока. Включение в цепь переменного тока катушки с индуктивностью L проявляется как увеличение сопротивления цепи. Объясняется это тем, что при переменном токе в катушке все время действует э. д. с. самоиндукции, ослабляющая ток. Сопротивление X_L, которое обусловливается явлением самоиндукции, называют индуктивным сопротивлением. Так как э. д. с. само­индукции тем больше, чем больше индуктивность цепи и чем быст­рее изменяется ток, то индуктивное сопротивление прямо пропорционально индуктивности цепи L и круговой частоте переменного тока ω: X_L = ωL.

Определим силу тока в цепи, содержащей катушку, активным сопротивлением которой можно пренебречь. Для это­го предварительно найдем связь между напряжением на катушке и ЭДС самоиндукции в ней. Если сопротивление катушки равно нулю, то и напряженность электрического поля внутри про­водника в любой момент времени должна быть равна нулю. Иначе сила тока, согласно закону Ома, была бы бесконечно большой.

Равенство нулю напряженности поля оказывается возможным потому, что напряженность вих­ревого электрического поля E_i, порождаемого переменным магнитным полем, в каждой точке равна по модулю и противоположна по направлению напряженности кулоновского поля Е_к, создаваемого в про­воднике зарядами, расположенными на зажимах источни­ка и в проводах цепи.

Из равенства E_i = -Е_к следует, что удельная работа вихревого поля (т. е. ЭДС самоиндукции e_i) равна по моду­лю и противоположна по знаку удельной работе кулонов­ского поля. Учитывая, что удельная работа кулоновского поля равна напряжению на концах катушки, можно запи­сать: e_i = -и.

При изменении силы тока по гармоническому закону i = I_m sin соsωt, ЭДС самоиндукции равна: е_i = -Li' = -LωI_m cos ωt. Так как e_i = -и, то напряжение на концах катушки ока­зывается равным

и = LωI_m cos ωt = LωI_m sin (ωt + π/2) = U_m sin (ωt + π/2)

гдеU_m = LωI_m — амплитуда напряжения.

Следовательно, колебания напряжения на катушке опе­режают по фазе колебания силы тока на π/2, или, что то же самое, колебания силы тока отстают по фазе от колеба­ний напряжения на π/2.

Амплитуда силы тока в ка­тушке равна:

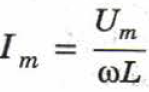
Если ввести обозначение X_L = ωL,то получим 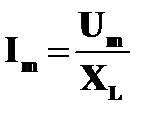. Величину X_L, равную произведению циклической час­тоты на индуктивность, называют индуктивным сопротив­лением. Согласно формуле 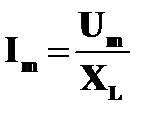, значение силы тока связано с значением напряжения и ин­дуктивным сопротивлением соотношением, подобным за­кону Ома для цепи постоянного тока.

Индуктивное сопротивление зависит от частоты ω. По­стоянный ток вообще «не замечает» индуктивности катушки. При ω = 0 индуктивное сопротивление равно нулю. Чем быстрее меняется напряжение, тем больше ЭДС са­моиндукции и тем меньше амплитуда силы тока. Следует отметить, что напряжение на индуктивном со­противлении опережает по фазе ток.

c) Конденсатор в цепи переменного тока. Постоянный ток не проходит через конденсатор, так как между его обкладками находится диэлектрик. Если конденсатор включить в цепь постоянного тока, то после зарядки конденсатора ток в цепи прекратится.

Пусть конденсатор включен в цепь переменного тока. Заряд конденсатора (q=CU) вследствие изменения напряжения непрерыв­но изменяется, поэтому в цепи течет переменный ток. Сила тока бу­дет тем больше, чем больше емкость конденсатора и чем чаще про­исходит его перезарядка, т. е. чем больше частота переменного тока.

Сопротивление, обусловленное наличием электроемкости в цепи переменного тока, называют емкостным сопротивле­нием Х_с. Оно обратно пропорционально емкости С и круговой частоте ω: Х_с=1/ωС.

Установим, как меняется со временем сила тока в цепи, содержащей только конденсатор, если сопротивлением прово­дов и обкладок конденсатора можно пренебречь.

Напряжение на конденсаторе u = q/C равно напряжению на концах цепи u = U_m cosωt.

Следовательно, q/C = U_m cosωt. Заряд конденсатора меняется по гармоническому закону:

q = CU_m cosωt.

Сила тока, представляющая со­бой производную заряда по вре­мени, равна:

i = q' = -U_mCω sin ωt =U_mωC cos(ωt + π/2).

Следовательно, колебания си­лы тока опережают по фазе ко­лебания напряжения на конден­саторе на π/2.

Амплитуда силы тока равна: Im = Um ωC. Если ввести обозначение Хс=1/ωС, то получим

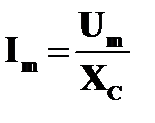
Величину Х_с, обратную произведению ωС циклической частоты на электрическую емкость конденсатора, называют емкостным сопротивлением. Роль этой величины анало­гична роли активного сопротивления R в законе Ома. Значение силы тока связано с значением напряжения на конденсаторе точно так же, как связаны согласно закону Ома сила тока и напряжение для участка цепи постоянного тока. Это и поз­воляет рассматривать величину Х_с как сопротивление кон­денсатора переменному току (емкостное сопротивление).

Чем больше емкость конденсатора, тем больше ток пе­резарядки. Это легко обнаружить по увеличению накала лампы при увеличении емкости конденсатора. В то время как сопротивление конденсатора постоянному току беско­нечно велико, его сопротивление переменному току имеет конечное значение Х_с. С увеличением емкости оно умень­шается. Уменьшается оно и с увеличением частоты ω.

В заключение отметим, что на протяжении четверти пе­риода, когда конденсатор заряжается до максимального напряжения, энергия поступает в цепь и запасается в кон­денсаторе в форме энергии электрического поля. В следую­щую четверть периода, при разрядке конденсатора, эта энергия возвращается в сеть.

Из сравнения формул X_L = ωL и Х_с=1/ωС видно, что катушки ин­дуктивности. представляют собой очень большое сопротивление для тока высокой частоты и небольшое для тока низкой частоты, а конденсаторы — наоборот. Индуктивное Х_L и емкостное Х_C сопротивления называют реактивными.

d) Закон ома для электрической цепи переменного тока.

Рассмотрим теперь более общий случай электрической цепи, в которой последовательно соединены проводник с активным сопротивлением R и малой индуктивностью, катушка с большой индуктивностью L и малым активным сопротивлением и конден­сатор емкостью С

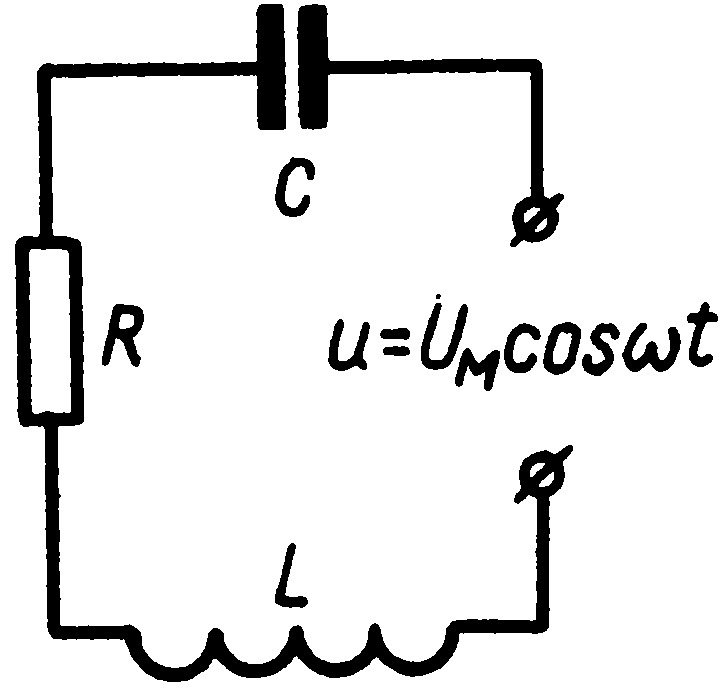
Чему равна амплитуда тока в такой цепи (колебательном кон­туре), если на ее концах поддерживается напряжение u(t) = Umcos ωt?

Мы видели, что при включении по отдельности в цепь активного сопротивления R, конденсатора емкостью С или катуш­ки с индуктивностью L амплитуда силы тока определяется соот­ветственно формулами:

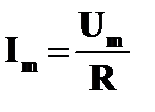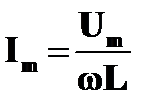; ; I_m = U_m ωC.

Амплитуды же на­пряжений на активном сопротивлении, катушке индуктивности и конденсаторе связаны с амплитудой силы тока так: U_m = I_mR; U_m = I_mωL;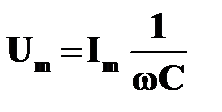

В цепях постоянного тока напряжение на концах цепи равно сумме напряжений на отдельных последовательно соединенных участках цепи. Однако, если измерить результирующее напряже­ние на контуре и напряжения на отдельных элементах цепи, ока­жется, что напряжение на контуре (действующее значение) не равно сумме напряжений на отдельных элементах. Почему это так? Дело в том, что гармонические колебания напряжения на различных участках цепи сдвинуты по фазе друг относительно друга.

Действительно, ток в любой момент времени одинаков во всех участках цепи. Это значит, что одинаковы амплитуды и фазы токов, протекающих по участкам с емкостным, индуктивным и активным сопротивлениями. Однако только на активном сопро­тивлении колебания напряжения и тока совпадают по фазе. На конденсаторе колебания напряжения отстают по фазе от колеба­ний тока на π/2, а на катушке индуктивности колеба­ния напряжения опережают колебания тока на π/2. Если учесть сдвиг фаз между складываемыми напряжениями, то окажется, что

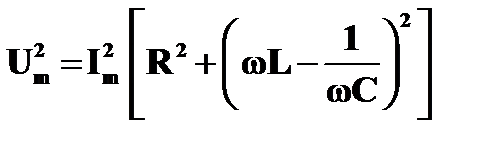
Для получения этого равенства нужно уметь скла­дывать колебания напряжений, сдвинутые по фазе друг относительно друга. Проще всего выполнить сложение нескольких гар­монических колебаний с помощью векторных диаграмм. Идея метода основана на двух довольно простых положениях.

Во-первых, проекция вектора с модулем х_m вращающегося с постоянной угловой скоростью совершает гармонические колебания: х = х_m cosωt

Во-вторых, при сложении двух векторов проекция суммарного векто­ра равна сумме проекций складываемых векторов.

Векторная диаграмма электрических колебаний в цепи, изображенной на рисунке, позволит нам получить соотношение между амплитудой силы тока в этой цепи и амплитудой напряжения. Так как сила тока одинакова во всех участках цепи, то построение век­торной диаграммы удобно начать с вектора силы тока I_m. Этот вектор изобра­зим в виде горизонтальной стрелки. Напряжение на активном со­противлении совпадает по фазе с силой тока. Поэтому вектор U_mR, должен совпадать по направлению с вектором I_m. Его модуль равен U_mR = I_mR

Колебания напряжения на индуктивном сопротивлении опережают колебания силы тока на π/2, и соответствующий вектор U_mL должен быть повернут относительно вектора I_m на π/2. Его модуль равен U_mL = I_m ωL. Если считать, что положительному сдвигу фаз соответствует поворот вектора против часовой стрелки, то вектор U_mL следует повернуть налево. (Можно было бы, конечно, поступить и наоборот.)

Вектор напряжения на конденсаторе UmC отстает по фазе от вектора Im на π/2 и поэтому повернут на этот угол относительно вектора Im направо.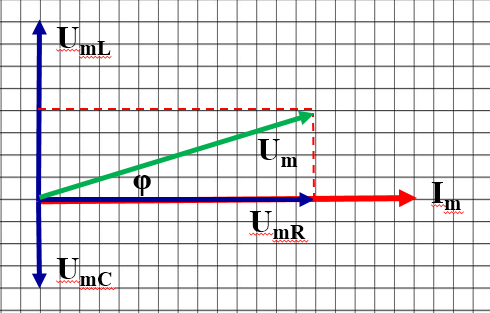

Его модуль равен U_mC =I_m/ωC. Для нахождения вектора суммарного напряжения U_m нужно сложить три вектора: 1) U_mR 2) U_mL 3) U_mC

Вначале удобнее сложить два вектора: U_mL и U_mC

Модуль этой суммы равен 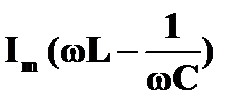, если ωL > 1/ωС. Именно такой случай изображен на рисунке. После этого, сложив вектор (U_mL + U_mC)с вектором U_mR получим вектор U_m, изображающий колебания напряжения в сети. По теореме Пифагора:

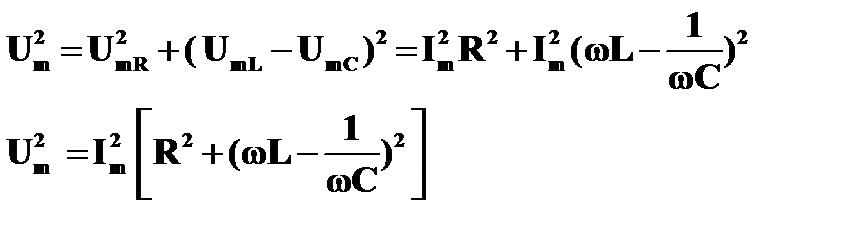
Из последнего равенства можно легко найти амплитуду силы тока в цепи:

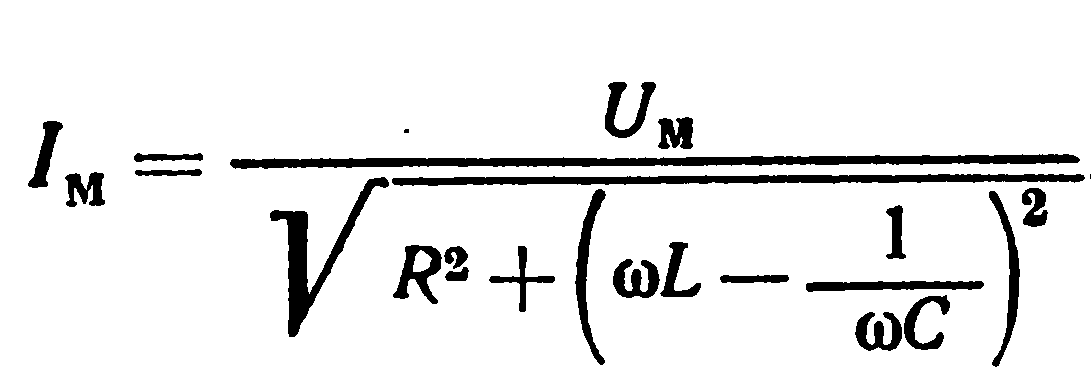
Таким образом, благодаря сдвигу фаз между напряжениями на различных участках цепи полное сопротивление Z цепи, изобра­женной на рисунке, выражается так:

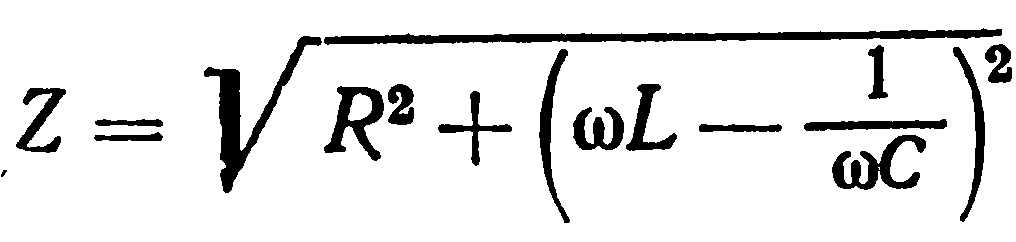
От амплитуд силы тока и напряжения можно перейти к дейст­вующим значениям этих величин:

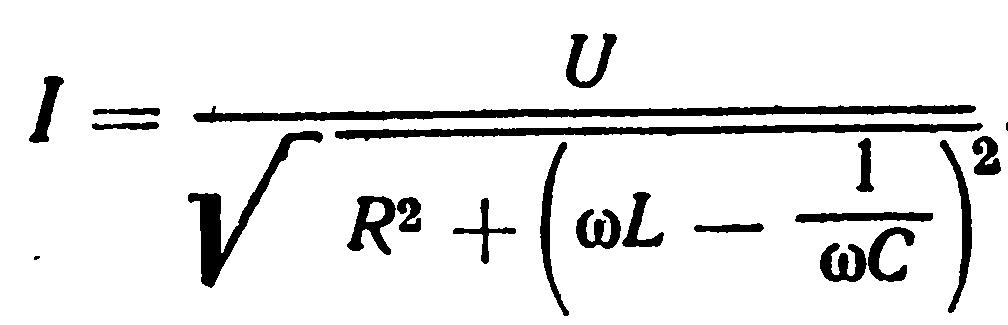
Это и есть закон Ома для переменного тока в цепи, изображен­ной на рисунке 43. Мгновенное значение силы тока меняется со временем гармонически:

i = I_m cos (ωt+ φ), где φ — разность фаз между силой тока и напряжением в сети. Она зависит от частоты ω и параметров цепи R, L, С.

e) Резонанс в электрической цепи.При изучении вынужденных механических колебаний мы по­знакомились с важным явлением — резонансом. Резонанс наблю­дается в том случае, когда собственная частота колебаний систе­мы совпадает с частотой внешней силы. При малом трении происходит резкое увеличение амплитуды установившихся вы­нужденных колебаний. Совпадение законов механи­ческих и электромагнитных ко­лебаний сразу же позволяет сделать заключение о возмож­ности резонанса в электриче­ской цепи, если эта цепь представляет, собой колеба­тельный контур, обладающий определенной собственной ча­стотой колебаний.

Амплитуда тока при вы­нужденных колебаниях в кон­туре, совершающихся под дей­ствием внешнего гармонически изменяющегося напряжения, определяется формулой:

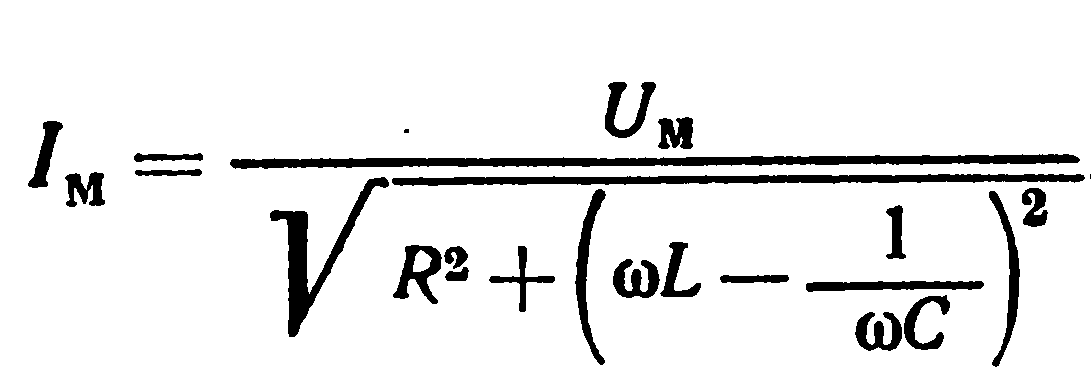
При фиксированном напря­жении и заданных значениях R, L и С, сила тока достигает мак­симума при частоте ω, удовлетворяющей соотношению

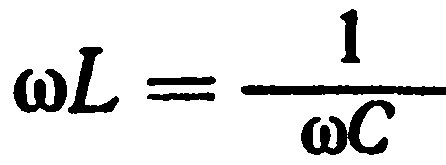
Эта амплитуда особенно велика при малом R. Из этого уравнения можно определить значение циклической частоты переменного тока, при которой сила тока максимальна:

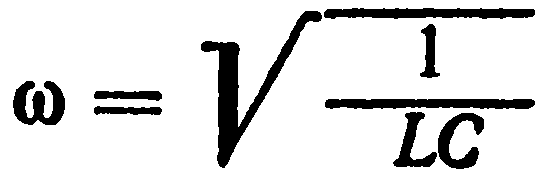
Эта частота совпадает с частотой свободных колебаний в конту­ре с малым активным сопротивлением.

Резкое возрастание амплитуды вынужденных колебаний тока в колебательном контуре с малым активным сопротивлением про­исходит при совпадении частоты внешнего переменного напря­жения с собственной частотой колебательного контура. В этом состоит явление резонанса в электрическом колебательном кон­туре.

Резонанс выражен тем отчетливее, чем меньше энергетиче­ские потери в цепи, т. е. чем меньше сопротивление R. При R = 0 резонансное значение тока неограниченно возрастает. Наоборот, с увеличением R максимальное значение тока умень­шается и при больших R говорить о резонансе уже не имеет смысла. Зависимость амплитуды силы тока от частоты при раз­личных сопротивлениях показана на рисунке.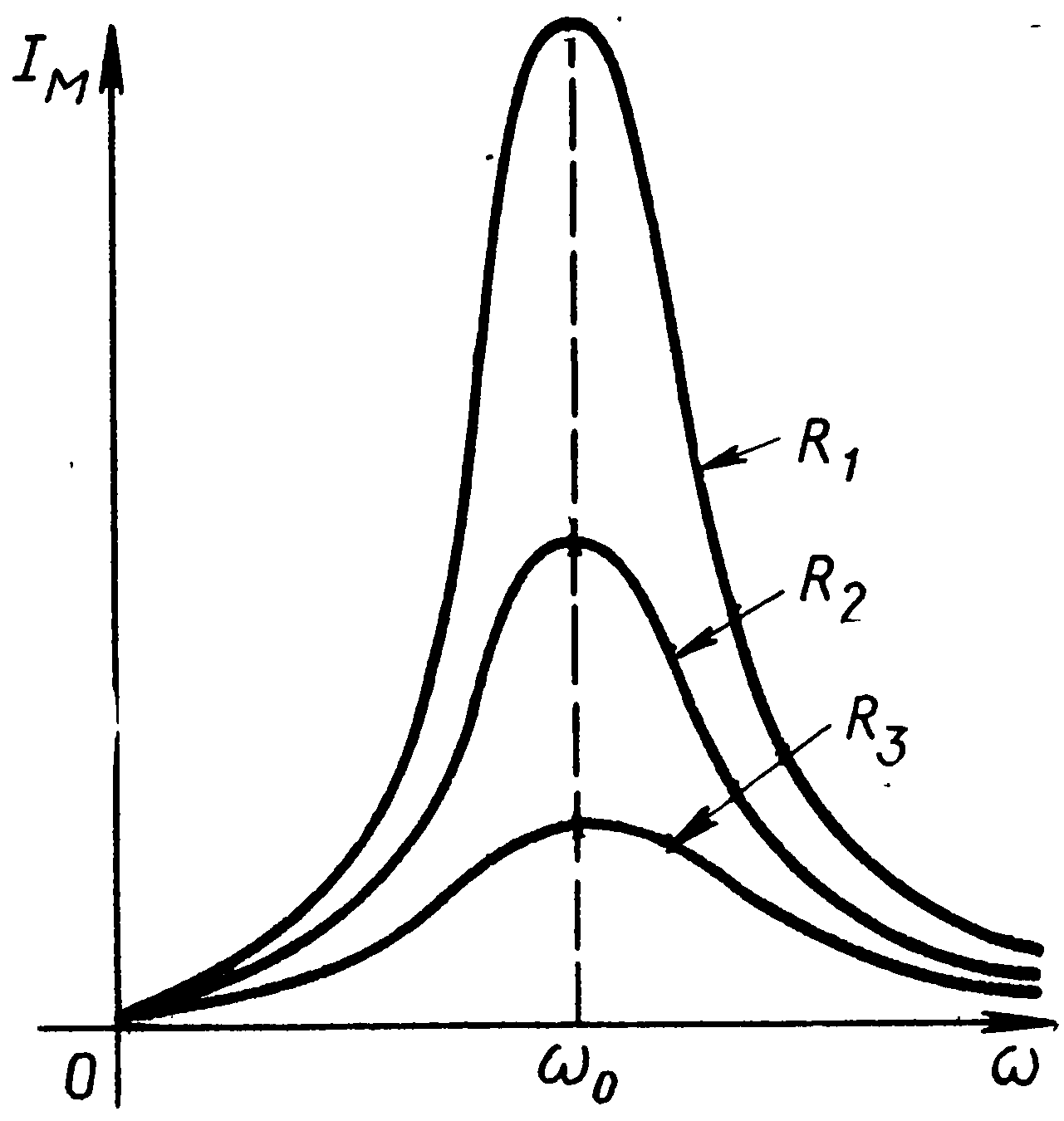

Одновременно с ростом силы тока при резонансе резко воз­растают напряжения на конденсаторе и катушке индуктивности. Эти напряжения становятся одинаковыми и во много раз пре­восходят внешнее напряжение.

Действительно,

U_{м, С,рез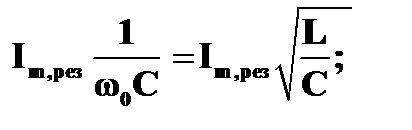} = U_{м, L,рез} =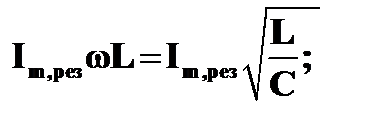

Внешнее напряжение связано с резонансным током так:

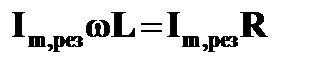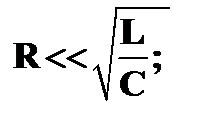U_м = .Если тоU_m,C,рез = U_m,L,рез >> U_m

При резонансе сдвиг фаз между током и напряжением стано­вится равным нулю.

Действительно, колебания напряжения на катушке индуктив­ности и конденсаторе всегда происходят в противофазе. Резо­нансные амплитуды этих напряжений одинаковы. В результате напряжения на катушке и конденсаторе полностью компенсиру­ют друг друга, и падение напряжения происходит только на активном сопротивлении.

Равенство нулю сдвига фаз между напряжением и током при резонансе обеспе­чивает оптимальные условия для поступления энергии от источ­ника переменного напряжения в цепь. Здесь полная аналогия с механическими колебаниями: при резонансе внешняя сила (ана­лог напряжения в цепи) совпадает по фазе со скоростью (аналог силы тока).