Анализ параллельной цепи переменного тока

При заданном гармоническом напряжении, ток в каждом элементе электрической цепи будет следующим:

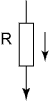UR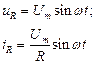

iR

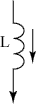UL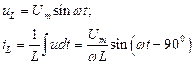

iL

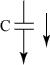
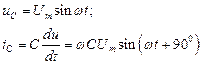
ic

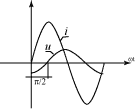
Объединим эти элементы в параллельную цепь и зададим ЭДС источника. Неизвестный ток этого источника найдём в виде i=I_m sin(ωt – φ) (рис.4.2.)

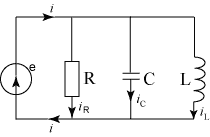
Рис.4.2.

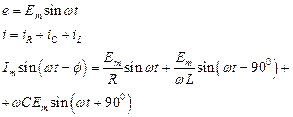
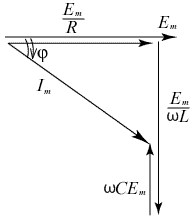
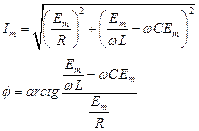
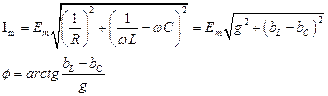
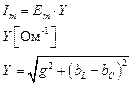Y – полная проводимость электрической цепи;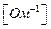

g – активная проводимость;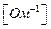

b_L – b_C – реактивная проводимость.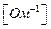

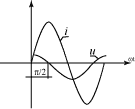
Напряжения, сопротивления и проводимости R, L, C при синусоидальном токе i = I_m sinωt

Таблица 4.1.

R	L	C

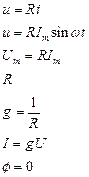
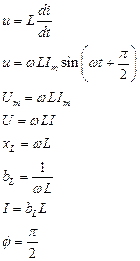
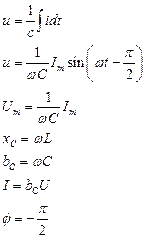
Таблица 4.2.Описание элементов R, L, C в комплексной форме.

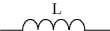
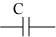
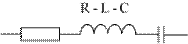
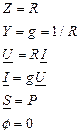
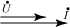
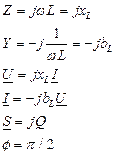
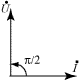
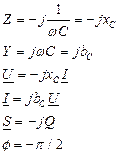
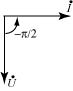
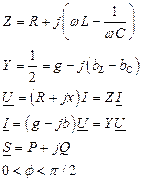
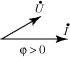
Основные формулы для расчёта цепей с последовательным и параллельным соединением элементовR, L, C

Таблица 4.3.

Последовательное соединение	Параллельное соединение

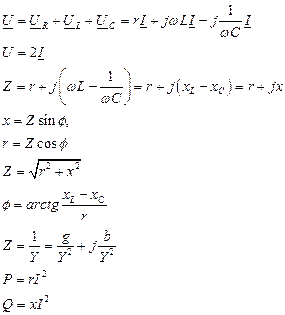
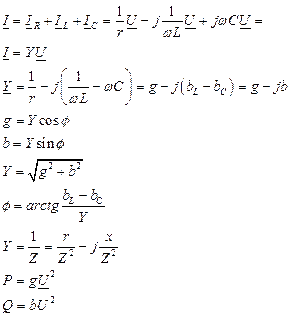
Лабораторная работа. Последовательное соединение элементов R, L, C

Цель работы – исследование электрической цепи с последовательным соединением элементов R, L, C при различных соотношениях индуктивного и емкостного сопротивлений.

Общие сведения

В работе сначала определяются параметры катушки методом амперметра, вольтметра и ваттметра при питании напряжения частоты f₁ = 50 Гц.

Схема для определения параметров катушки показана на рис.4.3.

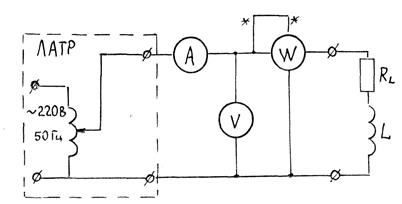
Рис.4.3

По изменённым значениям тока I_K, напряжения U_K и мощности P_K можно определить полное, активное и индуктивное сопротивления катушки по формулам

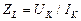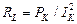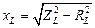, , , (4.1)

а также индуктивность и сдвиг по фазе между напряжением и током

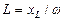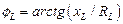; (4.2)

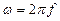- угловая частота.

При последовательном соединении элементов R, L, C полное сопротивление цепи определяется выражением

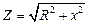(4.3)

где R–активное сопротивление цепи;

x – реактивное сопротивление цепи.

Реактивное сопротивление цепи при этом определяется выражением

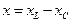(4.4)

где x_L = ωL – индуктивное сопротивление цепи;

x_C = 1/ωC – емкостное сопротивление цепи.

Действующее значение тока в цепи определяется выражением

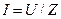(4.5)

где U – действующее значение напряжения на зажимах цепи.

При последовательном соединении R, L и C при определённых значениях x_L и x_C имеет место явление, называемое резонансом напряжения.

Резонансом напряжений называется такое состояние электрической цепи при последовательном соединении элементов R, L, C (рис.4.4.), когда сдвиг по фазе между напряжением на зажимах цепи и током в ней равен нулю, при этом x_L = x_C[1,2].

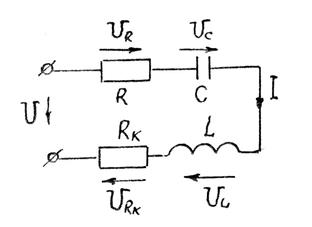
Рис. 4.4.

Напряжение на активном сопротивлении совпадает по фазе с током и равно

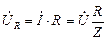(4.6)

Напряжение на емкости отстаёт от тока по фазе на 90⁰

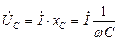(4.7)

Напряжение на индуктивности опережает ток на 90⁰

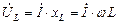(4.8)

Средняя мощность, расходуемая в цепи, определяется по формуле

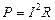(4.9)

Сдвиг фаз между напряжением на зажимах цепи и током в ней определяется выражениями:

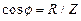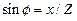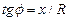; ; (4.10)

При резонансе cosφ = 1, а ток в цепи достигает максимального значения.

Если катушка индуктивности L имеет собственное сопротивление R_L, то падение напряжения на ней равно

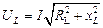(4.11)

При этом полное активное сопротивление цепи будет равно сумме внешнего сопротивления R₁ и собственного сопротивления катушки R_L

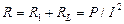
Векторная диаграмма напряжений и тока в цепи при индуктивном характере нагрузок показана на рис.4.5.

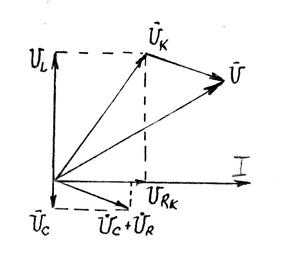
Рис.4.5.

При резонансе φ = 0, и, следовательно, x_L = x_C. При постоянных L и C это равенство имеет место на резонансной частоте

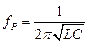или 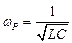(4.12)

Резонансное значение тока в цепи

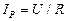(4.13)

Напряжение на активном сопротивлении R при резонансе равно напряжению источника питания.

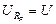(4.14)

Напряжение на емкости и на индуктивности при резонансе равны между собой

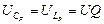(4.15)

где 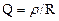- добротность контура;

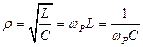- волновое или характеристическое сопротивление контура.

Средняя мощность при резонансе

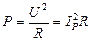(4.16)

Векторная диаграмма напряжений и токов при резонансе напряжений показана на рис. 4.6. Настроить цепь в резонансе с частотой источника питания можно также изменением индуктивности на ёмкости. Графики изменений тока в цепи, сдвига фаз и напряжений на элементах схемы при изменении частоты источника питания называются амплитудно-частотной (АЧХ) и фазо-частотной (ФЧХ) характеристиками контура и показаны на рис.4.7.

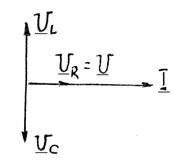
Рис.4.6.

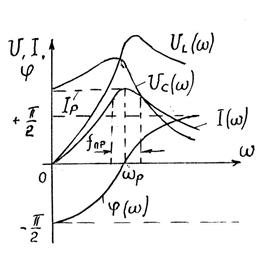
Рис.4.7.

Частотные характеристики могут быть построены по уравнениям (4.3 ÷ 4.11). Из выражения (4.5) следует

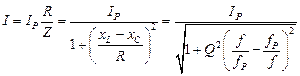(4.17)

Максимумы U_L и U_C достигаются при частотах, отличных от резонансной частоты ω_Р. U_{L max}наступает при частоте 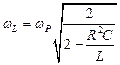, а U_{C max –} при частоте .

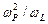Частотная характеристика тока позволяет экспериментально определить добротность контура.

Если определить полосу частот 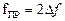, пропускаемых контуром на уровне 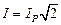, то добротность контура может быть найдена из выражения

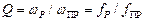(4.18)

На границах полосы пропускания сдвиг фаз между напряжением на зажимах цепи и током в ней составляет φ = ± 45⁰.

Содержание работы

1. пределение параметров катушки индуктивности методом амперметра, вольтметра и ваттметра при питании напряжением частоты 50 Гц.

2. следование электрической цепи с последовательным соединением резистора, катушки индуктивности и конденсатора при различных соотношениях индуктивного и емкостного сопротивлений.