Кинематический анализ манипулятора промышленного робота
Рассмотрим применение матричного метода для исследования шестизвенной открытой пространственной кинематической цепи механической руки ПР. С каждым звеном механизма свяжем прямоугольную систему координат (рис. 26).
Со стойкой – неподвижную систему координат 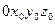 . Ось
. Ось 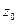 направим по оси вращения пары B.
направим по оси вращения пары B.
Со звеном 1 – систему координат 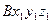 , которую сместим на величину
, которую сместим на величину 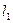 по оси
по оси 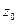 , параллельной оси
, параллельной оси 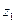 . Ось
. Ось 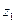 направлена по оси вращательной пары В, а ось
направлена по оси вращательной пары В, а ось 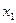 параллельно оси
параллельно оси 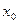 .
.
 |
Со звеном 2 свяжем систему координат
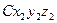 , смещенную на величину
, смещенную на величину 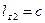 по оси
по оси 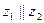 и повернутую на угол
и повернутую на угол 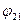 относительно этой оси.
относительно этой оси.
Со звеном 3 свяжем систему координат 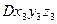 , смещенную на величину
, смещенную на величину 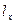 по оси
по оси 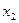 относительно системы
относительно системы 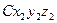 . Ось
. Ось 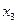 направим по оси
направим по оси 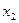 , а ось
, а ось 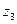 параллельно
параллельно 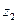 .
.
Со звеном 4 свяжем систему координат 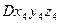 , повернутую относительно оси
, повернутую относительно оси 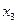 системы координат
системы координат 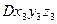 на угол
на угол 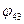 . Ось
. Ось 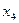 направим по оси
направим по оси 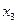 , а ось
, а ось 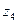 по оси вращения вращательной пары Е.
по оси вращения вращательной пары Е.
Со звеном 5 свяжем систему координат 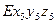 , смещенную на величину
, смещенную на величину 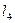 относительно системы координат
относительно системы координат 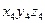 и повернутую на угол
и повернутую на угол 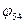 относительно оси
относительно оси 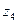 . Ось
. Ось 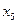 направим вдоль оси захвата 5.
направим вдоль оси захвата 5.
Задача о положениях точки F схвата 5 сводится к определению координат этой точки в системе 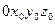 по известным координатам
по известным координатам 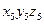 , известным линейным (
, известным линейным ( 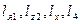 ) и угловым (
) и угловым ( 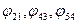 ) перемещениям звеньев.
) перемещениям звеньев.
Матричное уравнение для перехода от системы 5 к системе 4 запишется в виде:
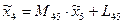 ,
,
где 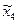 - координаты точки Е в системе
- координаты точки Е в системе 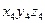 .
.
Матрица поворота и переноса имеет вид:
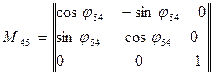 и
и 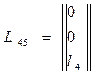
Матрица поворота при переходе от системы 4 к системе 3:
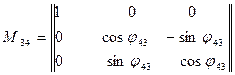
Матричное уравнение перехода к системе 3:
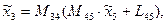
где 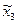 - координаты точки Е в системе
- координаты точки Е в системе 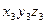 .
.
Матрица переноса от системы 3 к системе 2:
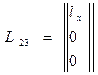
Матричное уравнение перехода к системе 2:
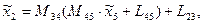
где 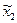 - координаты точки Е в системе
- координаты точки Е в системе 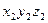 в форме матрицы-столбца.
в форме матрицы-столбца.
Матрицы поворота и переноса от системы 2 к системе 1 имеют вид:
 и
и 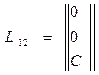
Матричное уравнение перехода к системе 1:
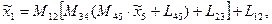
где 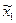 - матрица столбец координат точки Е в системе
- матрица столбец координат точки Е в системе 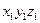 .
.
Матрица перехода к неподвижной системе 0:
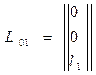
Матричное уравнение перехода к системе координат 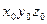 примет вид:
примет вид:
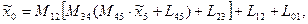
После некоторых преобразований находим выражение, связывающее координаты выбранной точки захвата в системах координат 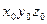 и
и 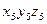 :
:
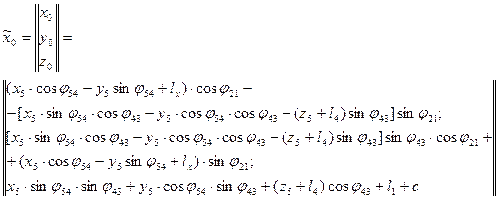
Общее решение задачи перехода от системы 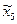 к системе
к системе 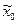 :
:
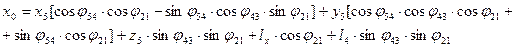
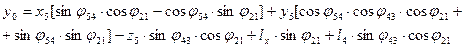
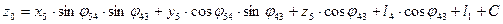
Кроме тех координат захвата, определяющих его положение, вычисляют три угла Эйлера или 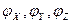 , дающие ориентацию захвата.
, дающие ориентацию захвата.
Матрица направляющих косинусов определяющих положение системы x 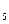 y
y 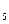 z
z 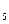 захвата относительно системы x
захвата относительно системы x 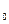 y
y 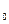 z
z 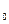 имеет вид:
имеет вид:
M 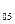 =M
=M 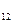 M
M 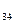 M
M  =
= 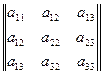


Дата добавления: 2017-05-02; просмотров: 1745;











