Динамика манипуляционных устройств

Динамика перемещения деталей роботом по каждой степени свободы движения состоит из этапов разгона, установившегося движения и торможения.

Обеспечение высокой скорости движений требует осуществления ускоренного разгона и торможения, что в свою очередь связано с возникновением больших динамических нагрузок, которые приводят к появлению колебательных движений звеньев робота, нарушению точности позиционирования, возникновению недопустимых деформаций и напряжений, особенно в период торможения.

При динамическом анализе конструкцию робота рассматривают как стержневую систему, нагруженную массой транспортируемой детали. Для получения достоверных теоретических выводов необходимо, чтобы расчетная схема обладала такими же энергетическими показателями, как и заданная реальная конструкция. Большая длина консольных звеньев и соизмеримость их массы с массой перемещаемых деталей требует обоснованного учета их в расчетной схеме. Исходя из того, что эти звенья представляют собой элементы с распределенной нагрузкой, то наиболее верным было бы представлять их в виде стержней с бесконечным числом степеней свободы. Сложность таких расчетов и несущественность получаемых при этом уточнений ограничивает целесообразность их выполнения, поэтому в расчетных схемах такие звенья заменяют невесомыми стержнями с некоторым числом сосредоточенных масс.

Обоснование необходимого числа заменяющих масс и их расположения по длине стержней выполняется на основе анализа частоты собственных колебаний, которая является наиболее важной характеристикой любой колебательной системы, так как она является функцией только параметров системы (жесткости и ее массы) и не зависит от амплитуды колебаний или способа, каким система приводится в движение. Для решения поставленных вопросов составляют исходную систему уравнений движения. Используя метод Даламбера и учитывая известные из механики соотношения между воздействующими на систему силами и перемещениями ее точек, уравнение движений при свободных колебаниях можно записать в форме:

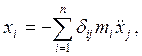
где 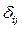- коэффициенты, учитывающие влияние перемещения масс в направлении 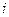от действия единичной силы в направлении ;

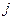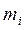- движущаяся масса;

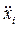- ускорение массы в 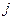-ом направлении;

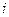- число степеней свободы.

Наиболее приемлемой расчетной схемой, дающей достаточно точные значения первых частот собственных колебаний при сравнительно невысокой сложности расчетов является система, в которой масса стержня принята в виде двух сосредоточенных масс по их концам.

Для роботов характерно, что частота его собственных колебаний является величиной переменной. Наибольшее влияние на частоту оказывает масса транспортируемой детали и вылет горизонтального плеча при повороте руки вокруг вертикальной оси.

Кривая 1 (рис. 27) показывает изменение основной гармоники колебаний системы с учетом массы детали 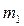, а кривая 2 – без учета массы 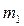. Изменение горизонтального вылета плеча оказывает большее влияние на частоту собственных колебаний. Наибольшая частота колебаний у роботов без нагрузки будет при среднем положении руки ( ).

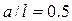При приложении нагрузки к плечу робота его частота колебаний будет уменьшаться. Максимальное значение частоты в этом случае будет уже в другом положении звеньев, но при том же условии, что ось вращения является главной центральной осью инерции системы.

Непостоянство частоты колебаний конструкции робота приводит к тому, что при одном и том же законе разгона и торможения в различных положениях руки точность позиционирования и быстрота перемещения руки с учетом выстоя для затухания колебаний будут неодинаковы. Поэтому для достижения одинаковой точности позиционирования и быстроты перемещения руки целесообразно корректировать характер движения в зависимости от величины вылета руки робота и действующей на него нагрузки.

Исследования показывают, что амплитуда колебаний и их продолжительность зависят от динамического качества конструкции робота (частоты собственных колебаний 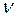и демпфирования 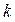) и характера остановки (начальной скорости и упругого смещения). Характер колебаний практически зависит только от частоты основной гармоники колебаний .

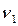Для уменьшения интенсивности колебаний, повышения точности и быстроты перемещения руки робота необходимо улучшать динамическое качество конструкции и осуществлять быстрое и плавное торможение с обеспечением минимальной начальной скорости и упругого смешения руки в момент остановки.