III. Расчёт электрического состояния цепи с последовательным соединением элементов L, R, C.

Рассмотрим цепь из трех последовательных токоприемников (рис. 2.12 а): пер­вые два имеют активно-индуктивный характер, третий является последователь­ным соединением резистора и конденсатора. Проведем анализ цепи по векторной диаграмме. Произвольно строим вектор тока, который является базовым для всех векторов диаграммы. В соответствии со вторым законом Кирхгофа

,

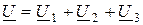где ; ; .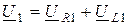

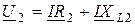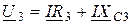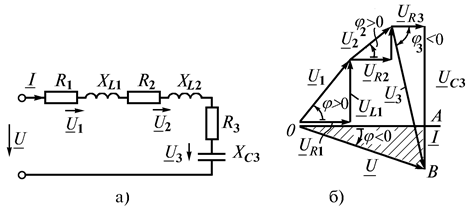
Рис. 2.12

Строим составляющие векторы, модули которых определяются по закону Ома. Суммарный вектор строим по правилу многоугольника. Векторы напряжений на активных сопротивлениях цепи совпадают по фазе с вектором тока, векторы 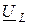опережают вектор тока на 90°, а вектор 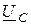отстает от него на угол 90° (рис. 2.12 б). Действующее значение напряжения источника (модуль вектора 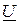) по диаграмме находится из треугольника напряжений ОАВ

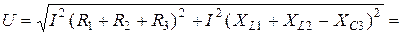
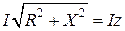. (2.27)

В формуле (2.27) 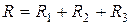– активное сопротивление цепи, равное арифметической сумме сопротивлений последовательно включенных резисторов. В общем случае для 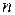последовательных приемников

.

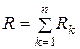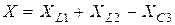является реактивным сопротивлением цепи, рав­ным алгебраической сумме реактивных сопротивлений последовательно вклю­ченных элементов. В общем случае

.

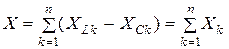В приведенной схеме сумма векторов индуктивных напряжений меньше век­тора напряжения на конденсаторе, поэтому 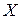< 0. В таком случае говорят, что реактивное сопротивление (или цепь в целом) носит емкостный характер.

Для проверки проводим расчёт активной и реактивной мощности и полной мощности P, Q и S:

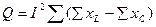U=UI