Произвольно расположенных в пространстве

Такое совмещение может быть осущестленно шестью элементарными поворотами и переносами, выполненными строго в следующей последовательности (повороты некоммутативны!)

1) поворот осей системы 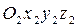вокруг оси 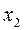до тех пор, пока ось 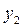не окажется в плоскости, параллельной плоскости осей ;

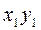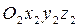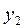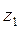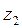2) поворот системы вокруг оси до тех пор, пока оси и не станут параллельными и одинаково направленными.

3) Поворот осей системы 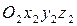вокруг оси 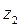до положения, при котором все оси систем 1 и 2 станут параллельны и одинаково направлены.

4) Последовательный перенос системы 2 вдоль осей 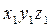, выполняемый в любой последовательности до полного совмещения осей координат.

Пример кинематического анализа манипулятора «Маскот-1»

Рассматриваемый манипулятор (рис. 25) имеет 6 степеней свободы и состоит из 6 подвижных звеньев, соединенных кинематическими парами V класса. С каждым звеном механизма связываем свою систему координат. Со стойкой - 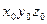, поместив ее начало в точке 0. Со звеном 1 – систему координат 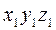, ось 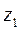параллельна 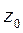; со звеном 2 - 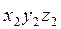, поместив начало в точке C; ось 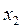направлена по оси звена 2, а ось 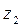- по оси вращательной пары C и т.д.

Пусть координатами произвольной точки А в системе координа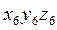т будут 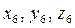(в дальнейшем их обозначим 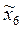). Координаты этой же точки в системе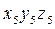

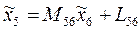
где 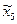, 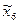- матрицы-столбцы координат точки А в системах координат 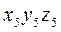и ;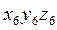

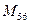- матрица поворота при переходе от системы 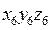к системе ;

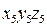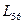- матрица параллельного переноса при переходе от системы 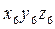к системе .

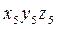Система 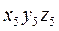может быть совмещена с системой 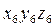поворотом вокруг оси 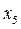на угол 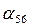. Поэтому

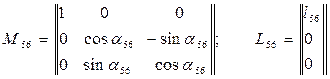
Системе координат 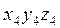может быть совмещена с системой 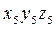поворотом оси 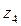на угол 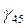. Матрица поворота при переходе от 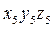к 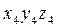имеет вид:

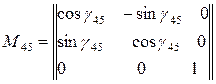
а матричное уравнение перехода к системе -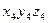

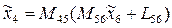
где 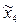- матрица-столбец координат точки А в системе .

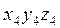Система координат 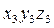может быть совмещена с 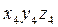переносом оси 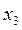на величину 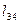и поворотом вокруг оси 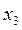на угол 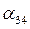. Матрица поворота при переходе от системы 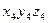к системе 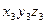имеет вид:

;

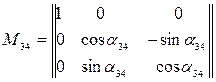Матрица переноса –

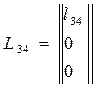
Матричное уравнение перехода к системе -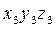

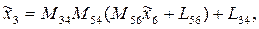
где 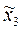- матрица-столбец координат точки А в .

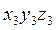Система 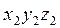может быть совмещена с 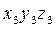поворотом вокруг оси 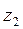на угол 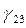. Матрица поворота при переходе от 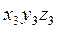к 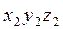имеет вид:

.

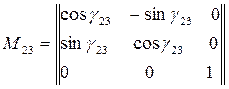Матричное уравнение перехода к системе -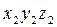

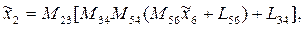
где 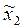- матрица-столбец координат точки А в системе .

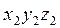Система 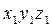может быть совмещена с 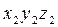переносом по оси 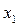на 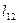и поворотом вокруг 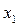на угол 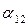. Матрица поворота при переходе от системы 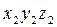к системе 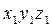записывается в форме:

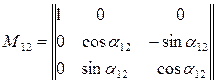
Матрица переноса –

,

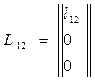Матричное уравнение перехода к системе -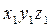

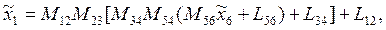
где 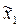- матрица-столбец координат О в системе .

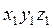Система 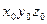может быть совмещена с системой 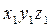поворотом вокруг оси 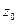на угол 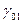. Матрица поворота при переходе от 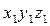к 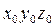имеет вид:

,

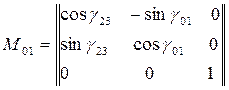Матричное уравнение перехода к системе -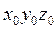

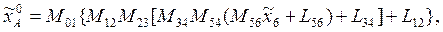
где 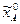- координаты точки А в системе .

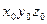Подставляя в последнее уравнение соответствующие матрицы M и L, получим выражения, связывающие координаты произвольной точки звена 6 в системах координат 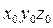и 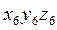. Введем обозначения обобщенных координат:

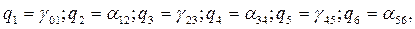
Тогда

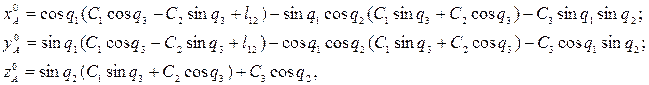где

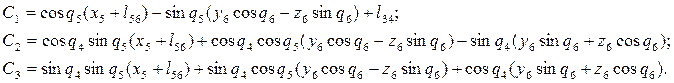При этом 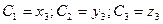- координаты точки А в системе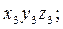 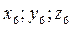- координаты А в системе 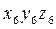; 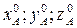- координаты точки А в системе 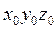. Для получения скоростей и ускорений можно дифференцировать матричное уравнение. Только зная 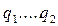, можно определить положение точки А, заданной в системе 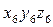, по отношению к системе 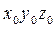.Скорости и ускорения точек схвата будут зависеть от скорости и ускорений обобщенных координат.