RLC-контур с параллельным соединением элементов в цепи переменного тока.

При анализе гармонических процессов в линейных электрических цепях переменного тока удобно пользоваться понятием «комплексное сопротивление»

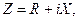(1)

где 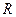- активное, 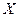- реактивное сопротивление участка цепи или цепи в целом. Значение реактивного сопротивления зависит от физических свойств элемента цепи и частоты переменного тока. Для ёмкости 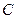и индуктивности 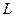в цепи переменного (гармонического) тока имеют место соотношения:

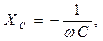
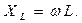(2)

Если таким величинам как сила тока и падение напряжения приписать физический смысл комплексных амплитуд гармонических колебаний, то первый и второй законы Кирхгофа можно использовать в форме, аналогичной стационарному случаю. В результате указанного приема удается рассчитать и величину (модуль вектора на векторной диаграмме) и начальную фазу колебаний рассматриваемой физической величины. При переходе к «действующим» величинам, естественно, отбрасывается информация о начальных фазах колебаний, а модули комплексных амплитуд колебаний уменьшаются в 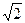раз.

Описанную выше методику применим к исследованию гармонических колебаний RLC-контура с параллельным соединением элементов, показанного на рис.1.

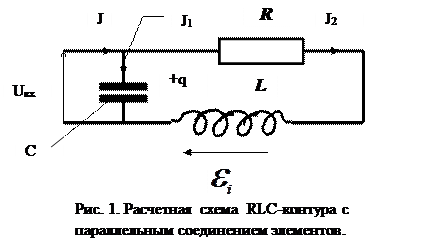
В силу первого закона Кирхгофа для выбранных положительных направлений токов имеем

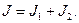(3)

В соответствии с определением (2) получим:

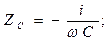
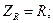
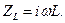(4)

Для последовательного соединения элементов цепи – активное сопротивление и индуктивность – запишем соотношение

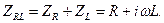(5)

В рассматриваемом случае легко видеть, что комплексные амплитуды сил токов на первом и втором участках цепи имеют вид

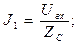
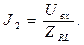(6)

Для полного тока в цепи (комплексная амплитуда силы тока) получаем с учетом соотношения (3):

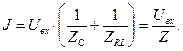(7)

Из зависимости (7) следует выражение для комплексного сопротивления параллельного соединения элементов цепи:

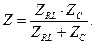(8)

Заметим, что выражение (8) по форме записи совпадает с аналогичным выражением для параллельного соединения элементов цепи постоянного тока.

Подытожим результаты:

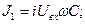
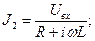
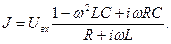(9)

С использованием соотношений (9) запишем выражения для действующих значений токов в элементах цепи:

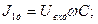
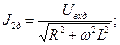
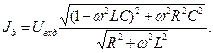(10)

В соотношениях (10) величина 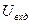является действующей (эффективной) величиной. Если рассматривать действующее значение силы тока в цепи 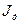как функцию круговой частоты вынуждающего воздействия 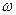, то можно рассчитать величину 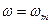, при которой сила тока 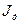в RLC-цепочке с параллельным соединением элементов будет минимальной. Получающееся выражение достаточно громоздко и неудобно для анализа. Более обозримые результаты имеют место для идеального контура в отсутствие активного сопротивления:

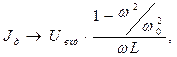
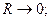
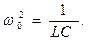(11)

Из соотношений (11) следует, что пр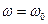и и 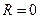в LC-цепочке с параллельным соединением элементов сила тока 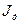обращается в нуль: электрическая схема не требует для своего функционирования внешней подпитки. Описанное явление имеет название «резонанс токов».