Алгебраическая сумма токов, текущих в участках цепи, соединённых в

Правила Кирхгофа.

Правила Г. Кирхгофа были установлены в 1845 году для стационарных токов в разветвленных электрических цепях сложной топологической структуры. Эти правила являются следствием закона сохранения электрического заряда и обобщенного закона Ома для участка цепи. Они позволяют задачу определения токов в отдельных участках сложной электрической цепи свести к хорошо изученной задаче линейной алгебры. В курсе общей физики для технических университетов достаточно выявить физическую сущность правил Кирхгофа: в последующем курсе электротехники, электрических машин и электроники описываются практические приёмы применения правил Кирхгофа к конкретным электрическим устройствам.

Любая электрическая схема сложной топологической структуры представляет собой некоторое конечное множество участков, концы каждого участка соединяются с концами некоторых других участков в узлах схемы. Участок представляет собой неразветвленный проводник, он может содержать ЭДС и характеризуется величиной электрического сопротивления. Узлом называют точку схемы, в которой соединяются концы не менее двух участков. При рассмотрении стационарных процессов, как правило, принимают, что узел схемы не обладает электрической ёмкостью. Важным понятием рассматриваемой теории является понятие «контур». Контур представляет собой замкнутую цепочку последовательно соединённых участков электрической схемы. Для реальной электрической схемы число контуров ограничено.

На первом этапе расчёта электрической схемы произвольным образом пронумеруем все участки электрической схемы, пронумеруем все узлы электрической схемы, зададим направления токов в каждом проводнике и зададим положительные направления обхода каждого контура электрической схемы. В результате первого этапа оказываются определёнными знаки алгебраических величин ЭДС на каждом участке схемы: полагаем ЭДС положительной величиной, если направление от отрицательной клеммы источника тока к положительной клемме совпадает с положительным направлением обхода рассматриваемого контура. Заметим, что одна и та же ЭДС фиксированного участка схемы может оказаться одновременно и положительной и отрицательной величиной в зависимости от того, в каком контуре рассматривается этот участок. Ещё одним результатом первого этапа является возможность определить для каждого узла схемы, электрический ток конкретного участка по отношению к рассматриваемому узлу является «входящим» (направлен к узлу) или «выходящим» (направлен из узла). Удобно в первом случае считать ток положительным, а во втором – отрицательным. Заметим, что один и тот же ток по отношению к одному узлу может быть положительным, а по отношению к другому – отрицательным. Поскольку участок цепи соединяет только два узла, то рассматриваемый ток по отношению к соединяемым узлам обязательно должен иметь разные знаки (из одного узла ток исходит, а в другой узел приходит).

Далее следует оговорить, что ниже рассматриваем стационарные процессы, в которых физические величины не претерпевают изменения с течением времени.

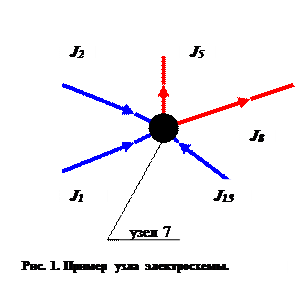
Первое правило Кирхгофа. Поскольку в каждом узле электрической схемы не должен накапливаться электрический заряд, то в соответствии с законом сохранения электрического заряда сумма всех входящих в рассматриваемый узел токов должна равняться сумме всех выходящих из узла токов.

С учётом знаков алгебраических величин закон сохранения электрического заряда можно сформулировать в следующей форме:

Алгебраическая сумма токов, текущих в участках цепи, соединённых в

рассматриваемый узел, равняется нулю.

Математическая формулировка первого правила Кирхгофа имеет вид:

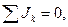для каждого узла схемы. (1)

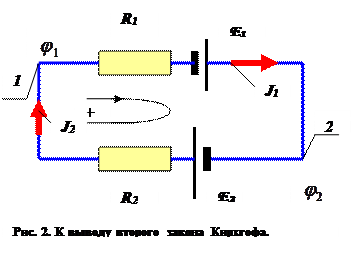
Второе правило Кирхгофа. Второе правило Кирхгофа основано на последовательном применении обобщённого закона Ома к участкам электрической цепи, составляющих один из контуров схемы. Для наглядности и упрощения выкладок рассмотрим простейший контур из двух участков (кольцо с двумя узлами). Физические величины, относящиеся к первому участку, снабдим индексом 1, а ко второму участку – индексом 2. 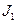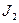Пусть токи и для определенности совпадают с положительным направлением обхода рассматриваемого контура. На первом участке ток течёт от узла 1 к узлу 2, на втором участке ток течёт от узла 2 к узлу 1.

В соответствии с обобщённым законом Ома в интегральной форме запишем для первого и второго участка цепи соответственно: 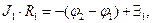(2)

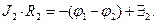(3)

В соотношениях (2) и (3) величины ЭДС условно записаны как положительные. Складывая левые и правые части рассматриваемых соотношений, получим: 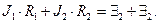(4)

В общем случае число участков контура может быть не равно двум, выбранные направления токов могут не совпадать с выбранным положительным направлением обхода контура, ЭДС каждого участка контура может быть или положительной, или отрицательной величиной. В любом случае рассматриваемый метод приводит к результату, аналогичному соотношению (4):

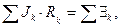для каждого контура. (5)

Соотношение (5) является математической формулировкой второго правила Кирхгофа: