Формулы расчета численности выборки

№	Тип выборки	Оцениваемый параметр	Повторный отбор	Бесповторный или механический отбор
1.	Собственно-случайная и механическая выборки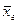
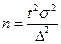
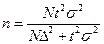
p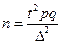
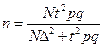
2.	Типическая (стратифицированная) выборка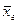
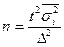
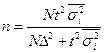
p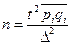
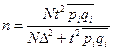
3.	Серийная (гнездовая) выборка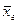
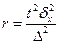
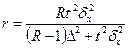
p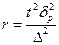

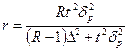
Для определения необходимой численности выборки должны быть заданы предельная ее ошибка, вероятность того, что эта ошибка не превысит заданного предела, а также иметься информация о дисперсии изучаемого признака в генеральной совокупности.

В практике исследований величина предельной ошибки выборки, как правило, устанавливается не в абсолютном, а в относительном выражении:

,

,

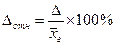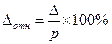причем ее величина для обеспечения репрезентативности выборки, как правило, не должна превышать 5%.

Тогда абсолютная величина предельной ошибки выборки может быть определена по следующим формулам:

,

.

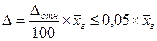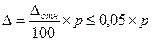Зачастую в практике исследований имеют место случаи, когда на этапе разработки программы выборочного обследования нет точной информации о вариации изучаемого признака. В таких случаях (т.е. до проведения обследования) приближенно оценить дисперсию или среднее квадратическое отклонение можно следующим образом:

· исходя из результатов специально организованного пробного обследования;

· опираясь на данные предыдущих обследований, как выборочных, так и сплошных. К примеру, если из предыдущих исследований имеется информация о коэффициенте вариации (V), то дисперсия может быть определена следующим образом:

;

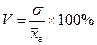
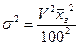· исходя из закона распределения изучаемого признака в генеральной совокупности, к примеру, если распределение изучаемого признака близко к нормальному, то среднее квадратическое отклонение в 6 раз меньше размаха вариации.

Если дисперсия доли единиц генеральной совокупности, обладающих определенным значением альтернативного признака, неизвестна, то при определении объема выборки можно использовать максимальное ее значение 0,25 (при p=q=0,5). Однако в данном случае объем выборки существенно возрастет, что приведет к значительному увеличению трудоемкости выборочного обследования.

Уровень надежности результатов выборочного обследования или вероятность того, что предельная ошибка не превысит заданного предела, задается, как правило, равной 0,95 и выше, что обуславливается необходимостью обеспечения практической ценности результатов выборочного обследования.