II.1.1 ОСНОВНЫЕ ЗАКОНЫ И ФОРМУЛЫ
1. Средняя скорость 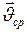 материальной точки:
материальной точки:
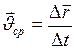 , или
, или 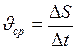 , (II.1)
, (II.1)
где 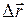 - элементарное приращение точки за промежуток времени
- элементарное приращение точки за промежуток времени  ;
;
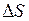 - путь, пройденный точкой за промежуток времени
- путь, пройденный точкой за промежуток времени  .
.
2. Мгновенная скорость 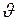 материальной точки:
материальной точки:
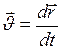 , или
, или 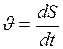 . (II.2)
. (II.2)
где 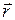 - радиус-вектор точки.
- радиус-вектор точки.
3. Среднее ускорение 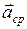 материальной точки:
материальной точки:
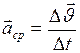 . (II.3)
. (II.3)
4. Мгновенное ускорение  материальной точки:
материальной точки:
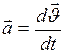 . (II.4)
. (II.4)
5. Скорость для прямолинейного равномерного движения:
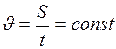 . (II.5)
. (II.5)
6. Путь и скорость для прямолинейного равнопеременного движения:
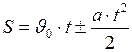 ; (II.6)
; (II.6)
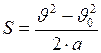 ; (II.7)
; (II.7)
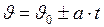 , (II.8)
, (II.8)
где 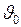 - начальная скорость.
- начальная скорость.
В уравнениях (II.6) и (II.8) ускорение положительно при равноускоренном движении и отрицательно при равнозамедленном.
7. Полное ускорение при криволинейном движении
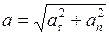 , (II.9)
, (II.9)
где 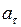 - тангенциальное ускорение;
- тангенциальное ускорение;
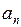 - нормальное (центростремительное) ускорение.
- нормальное (центростремительное) ускорение.
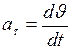 ; (II.10)
; (II.10)
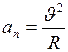 , (II.11)
, (II.11)
где 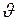 - скорость движения материальной точки;
- скорость движения материальной точки;
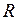 - радиус кривизны траектории в данной точке.
- радиус кривизны траектории в данной точке.
При вращении тела угол 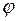 есть величина переменная, зависящая от времени
есть величина переменная, зависящая от времени 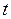 .
.
8. Выражение вида 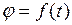 называется кинематическим уравнением вращения.
называется кинематическим уравнением вращения.
9. Средняя угловая скорость 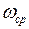 материальной точки:
материальной точки:
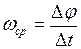 , (II.12)
, (II.12)
где 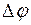 - изменение угла поворота за время
- изменение угла поворота за время  .
.
10. Мгновенная угловая скорость 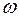 материальной точки:
материальной точки:
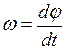 . (II.13)
. (II.13)
11. Среднее угловое ускорение 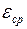 материальной точки:
материальной точки:
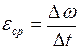 , (II.14)
, (II.14)
где 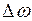 - изменение угловой скорости за время
- изменение угловой скорости за время  .
.
12. Мгновенное угловое ускорение 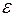 материальной точки:
материальной точки:
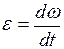 . (II.15)
. (II.15)
13. Уравнение равномерного вращения:
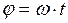 . (II.16)
. (II.16)
14. Угловая скорость при равномерном вращательном движении:
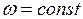 . (II.17)
. (II.17)
15. Угловое ускорение при равномерном вращательном движении:
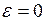 . (II.18)
. (II.18)
16. Уравнение равнопеременного вращения:
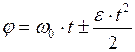 . (II.19)
. (II.19)
17. Угловая скорость равнопеременного вращения:
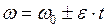 . (II.20)
. (II.20)
18. Угловое ускорение равнопеременного вращения:
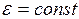 . (II.21)
. (II.21)
19. Частота вращения (число оборотов в единицу времени):
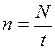 , (II.22)
, (II.22)
или
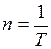 , (II.23)
, (II.23)
где 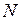 - число оборотов, совершаемых за время
- число оборотов, совершаемых за время 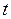 ;
;
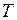 - период вращения (время одного полного оборота).
- период вращения (время одного полного оборота).
20. Связь между линейными и угловыми величинами выражается следующими формулами:
а) длина дуги, пройденная материальной точкой:
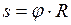 , (II.24)
, (II.24)
где 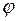 - угол поворота тела;
- угол поворота тела; 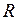 - радиус вращения точки.
- радиус вращения точки.
б) линейная скорость точки:
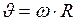 ; (II.25)
; (II.25)
в) тангенциальное ускорение точки:
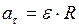 ; (II.26)
; (II.26)
г) нормальное ускорение точки:
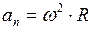 . (II.27)
. (II.27)
Дата добавления: 2016-09-06; просмотров: 3060;











