Оценка параметров генеральной совокупности по малым выборкам
На практике зачастую в ходе выборочного исследования нецелесообразно или нет возможности использовать выборки повышенного объема, что связано с утерей в ходе обследования изучаемых свойств единицами наблюдения. К примеру, исследуется прочность изделия, средняя продолжительность его эксплуатации и т.д. В данных случаях целесообразно использование выборок небольшого объема – малых выборок.
В статистике выборка считается малой, если ее объем n < 20÷30. Использование малых выборок при выборочном наблюдении имеет следующие особенности:
1) необоснованным становится вывод о нормальном законе распределения выборочных средней 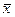 и доли w, так как он основан на центральной предельной теореме при больших значениях n [10];
и доли w, так как он основан на центральной предельной теореме при больших значениях n [10];
2) необоснованной становится замена неизвестных генеральной дисперсии σ2 и доли р их точечными оценками соответственно s2 и w, так как в силу состоятельности данных оценок эта замена возможна лишь при больших n.
В случае малых выборок оценка генеральной средней и доли осуществляется следующим образом.
1. Оценка генеральной средней.
В теории математической статистики доказано, что по данным выборки можно построить случайную величину
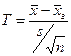 ,
,
которая имеет распределение Стьюдента с 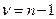 степенями свободы. Функция плотности распределения Стьюдента имеет следующий вид:
степенями свободы. Функция плотности распределения Стьюдента имеет следующий вид:
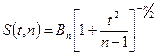 ,
,
где 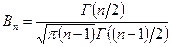 ;
; 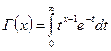 - гамма-функция;
- гамма-функция;
t – возможные реализации случайной величины T; n – объем выборки.
Тогда доверительную вероятность (и доверительный интервал соответственно), т.е. вероятность попадания оцениваемой величины в заданный интервал можно определить на основе функции распределения Стьюдента[11]:
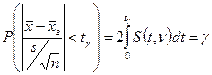 ,
,
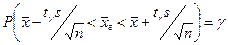
2. Оценка генеральной доли (вероятности биномиального распределения).
Границы p1 и p2 доверительного интервала для генеральной доли (для случая повторного отбора) можно определить по следующим формулам:
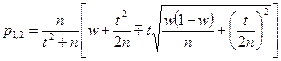 .
.
В случае больших выборок, при 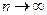 , в вышеприведенной формуле величинами
, в вышеприведенной формуле величинами 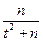 (по сравнению с 1),
(по сравнению с 1), 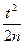 (по сравнению w) и
(по сравнению w) и 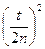 (по сравнению с
(по сравнению с 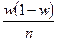 ) можно пренебречь, в результате чего данную формулу можно упростить следующим образом:
) можно пренебречь, в результате чего данную формулу можно упростить следующим образом:
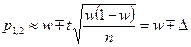 .
.
Дата добавления: 2017-05-02; просмотров: 1606;











