Выборочный линейный коэффициент корреляции К. Пирсона

На основе аналитических группировок и корреляционных таблиц можно не только выявить наличие зависимости между двумя коррелируемыми показателями, но и измерить тесноту этой связи, в частности, с помощью линейного коэффициента корреляции r.

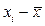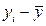При расчете этого показателя учитываются не только знаки отклонений индивидуальных значений признака от средней, но и сами величины таких отклонений, т.е. и . Однако непосредственно сопоставить между собой полученные абсолютные величины нельзя, т.к. сами признаки могут быть выражены в разных единицах, а при наличии одних и тех же единиц измерения средние могут быть различны по величине. В этой связи сравнению могут подлежать отклонения, выраженные в относительных величинах, к примеру, в долях среднего квадратического отклонения (их называют нормированными отклонениями).

Так для факторного признака будем иметь совокупность величин 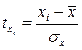, а для результативного .

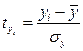Для получения обобщающей характеристики степени тесноты связи между признаками рассчитывают среднее произведение нормированных отклонений, полученная величина и является линейным коэффициентом корреляции:

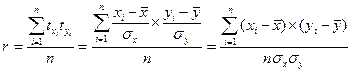. (9.2)

Величину, расположенную в числителе, называют ковариацией или корреляционным моментом:

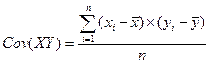. (9.3)

Вычисление коэффициента корреляции по формуле (9.2) является трудоемкой операцией, поэтому на практике используют следующую формулу:

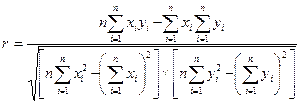. (9.4)

Если исходная информация сгруппирована и подсчитаны частоты повторений пар исследуемых признаков, то для расчета линейного коэффициента корреляции используют взвешенную формулу:

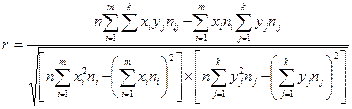. (9.5)

На основе аналитических группировок и корреляционных таблиц можно не только выявить наличие зависимости между двумя коррелируемыми показателями, но и измерить тесноту этой связи, в частности, с помощью эмпирического корреляционного отношения:

,

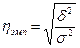и эмпирического коэффициента детерминации:

,

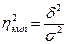где 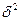и 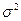соответственно межгрупповая и общая дисперсии результативного признака.

Для нашего примера данные показатели будут равны:

.

.

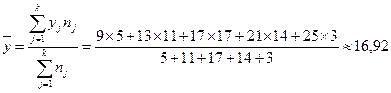
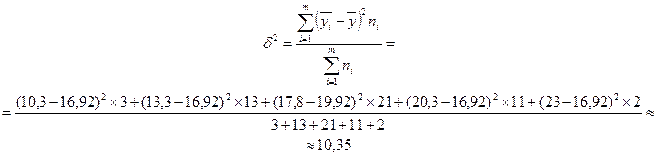
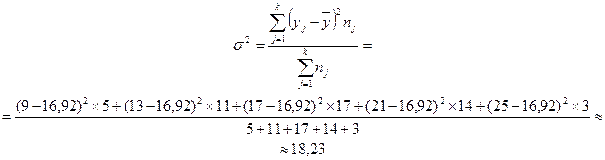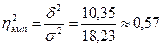Эмпирический коэффициент детерминации характеризует, что вариация зависимого результативного признака (суточной выработки продукции) только на 57% объясняется вариацией независимого признака (основных производственных фондов предприятий). Остальные 43% – действие прочих неучтенных факторов.

.

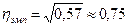Значение эмпирического корреляционного отношения (учитывая, что связь между X и Y – прямая, значение 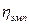взято со знаком «+») характеризует тесноту связи выше средней, поэтому можно сделать вывод о наличии существенной прямой связи между суточной выработкой продукции и стоимостью основных производственных фондов.