Сущность причинно-следственной связи, ее виды

Исследование объективно существующих связей между явлениями – важнейшая задача статистики, причем под социально-экономическим явлением понимают определенный признак или их совокупность, позволяющие всесторонне охарактеризовать данное явление с точки зрения поставленных целей исследования.

Для целей исследования взаимосвязей между явлениями всю совокупность признаков, характеризующих данные явления, условно можно подразделить на две группы:

1) признаки, рассматриваемые как факторы воздействия (признаки-факторы или факторные признаки), как правило, обозначают через Х;

2) признаки, рассматриваемые как результат воздействия факторов (признаки-результаты или результативные признаки), как правило, обозначают через Y.

Под причиной будем понимать совокупность определенных значений факторных признаков, характеризующих явления-причины, и, приводящих к появлению определенных значений результативных признаков, которые характеризуют явление-следствие.

В процессе статистического исследования взаимосвязи социально-экономических явлений вскрываются причинно-следственные отношения между данными явлениями, т.е. связь явлений, когда изменение одних (причины) приводит к изменению других (следствию). Причем, как правило, социально-экономические явления представляют собой результат одновременного воздействия большого числа причин. Следовательно, при изучении данных явлений необходимо уметь выявлять основные и второстепенные причины, изучать их влияние в совокупности, а также исследовать влияние основных причин, абстрагируясь от второстепенных. Необходимо также отметить, что один и тот же признак (явление) в одних причинно-следственных отношениях может выступать в качестве факторного признака, а в других – в качестве результативного.

Особенностью причинно-следственных связей социально-экономиче­ских явлений является их транзитивность, т.е. причина X и следствие Y свя­заны через множество промежуточных факторов условно 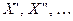и т.д., а не непосредственно 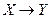. Од­нако промежуточные факторы, как правило, при анализе опускаются в силу сложности или невозможности их учета.

Таким образом, выражаясь в терминах статистики, статистическое исследование взаимосвязи социально-экономических явлений предполагает изучение влияния факторных признаков, характеризующие явления-причины, на вариацию результативных признаков, характеризующих явление-результат.

В статистике принято выделять следующие виды причинно-следственной связи: 1) функциональная связь; 2) стохастическая (вероятностная) связь; 3) статистическая связь; 4) корреляционная связь.

Функциональной называют связь, при которой каждому конкретному значению факторного признака соответствует одно или несколько определенных значений результативного признака. Функциональная связь двух величин возможна лишь при условии, что вторая из них на 100% зависит только от первой и ни от чего более.

Функциональная связь чаще встречается в точных науках, например, площадь квадрата характеризуется следующей функциональной связью: 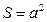. При увеличении, к примеру, стороны квадрата в два раза, его площадь увеличиться в 4 раза. Другой пример функциональной связи: 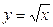(в данном случае, к примеру, значению 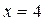соответствует два значения: 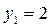и ).

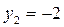Пример функциональной связи в экономике: при простой сдельной оплате труда связь между оплатой труда y и количеством изготовленных изделий x при фиксированной расценке за одну деталь, например 5 руб., можно выразить формулой: .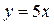

Стохастической (вероятностной) называют связь, при которой каждому значению факторного признака соответствует определенное распределение вероятностей появление того или иного значения результативного признака.

Статистической называют связь, при которой каждому значению факторного признака соответствует определенное статистическое (выборочное) распределение результативного признака. Статистическая связь является частным случаем стохастической, она устанавливается на основе выборочных данных.

Корреляционной называют связь, при которой каждому значению факторного признака соответствует условное среднее значение результативного признака. Корреляционная связь является частным случаем статистической связи. В статистике различают следующие виды корреляционной связи:

а) парная корреляция – связь между результативным и одним факторным признаками;

б) частная корреляция – связь между результативным и одним факторным признаками, при фиксированных значения других факторных признаков;

в) множественная корреляция – связь между результативным и двумя или более факторными признаками.

Взаимосвязь явлений удобно представлять в табличной и графической формах.

Таблицу, в которой значениям результативного признака соответствуют значения факторных признаков называют корреляционной таблицей (от лат. correlatio – соотношение, взаимосвязь) Корреляционным полем называют график, представляющий совокупность точек с координатами ( 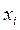, 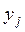). Эмпирической линией регрессии(от лат. regressio – движение назад) называют ломанную, вершины которой имеют координаты ( , ).

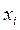Кроме того, выделяют прямую и обратную, а также линейную и нелинейную причинно-следственную связь.

Прямой называют связь, при которой с увеличением значений факторных признаков, значения результативного также возрастают и наоборот.

Обратной называют связь, при которой с увеличением значений факторных признаков, значения результативного – убывают, и наоборот.

Линейной называют связь, при которой одинаковым приращениям факторных признаков соответствуют одинаковые приращения результативного. Линейная связь характеризуется следующей аналитической зависимостью: .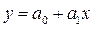

Нелинейной называют связь, при которой одинаковым приращениям факторных признаков соответствуют неодинаковые приращения результативного. Например, нелинейная связь может характеризоваться параболической зависимостью ( 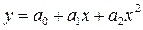), гиперболической ( 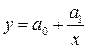) и др.

Укрупненно схему статистического исследования взаимосвязи между изучаемыми явлениями можно представить последовательностью следующих этапов:

1. Качественный анализ изучаемого социально-экономического явления, связанный с анализом его природы методами экономической теории, социологии и др.;

2. Построение модели корреляционной связи, используя статистический инструментарий:

2.1. Выявление наличия (или отсутствия) корреляционной связи между изучаемыми признаками и измерение тесноты связи между двумя (и более) признаками. Данную часть исследования называют корреляционным анализом.

2.2. Определение уравнения регрессии – математической модели, в которой среднее значение результативного признака рассматривается как функция одной или нескольких переменных – факторных признаков. Данная часть исследования называется регрессионным анализом.

3. Интерпретация результатов.