II.5.1 ОСНОВНЫЕ ЗАКОНЫ И ФОРМУЛЫ

1. Закон всемирного тяготения

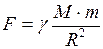, (II.76)

где 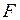- сила взаимного притяжения двух тел, размерами которых можно пренебречь по сравнению с расстоянием между ними;

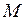и - массы тел; 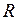- расстояние между ними;

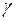- гравитационная постоянная.

Два шара со сферически симметричным распределением плотности вещества в каждом шаре притягивают друг друга так, как будто вся масса каждого шара сосредоточена в его центре.

2. Напряжённость гравитационного поля

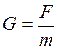, (II.77)

где 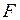- сила тяготения, действующая на материальную точку массой , помещённую в данную точку поля.

Если гравитационное поле, напряжённость которого мы определяем, само создано материальной точкой или телом со сферически симметричным распределением плотности, то

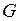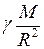= , (II.78)

где 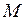- масса материальной точки (тела, создающего поле);

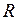- расстояние от неё до интересующей нас точки поля.

3. Ускорение свободного падения 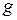на высоте 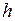над поверхностью Земли

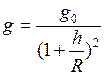, (II.79)

где 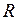- радиус Земли; 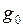- ускорение на поверхности Земли.

Если 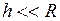, то

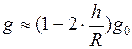. (II.80)

4. Потенциальная энергия гравитационного взаимодействия двух материальных точек всегда отрицательна и выражается формулой

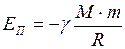, (II.81)

где 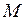и - массы материальных точек; 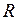- расстояние между ними.

При 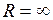потенциальная энергия системы имеет максимальное значение, равное нулю.

5. Работа сил гравитационного поля при сближении двухматериальных точек равна уменьшению потенциальной энергии тяготения

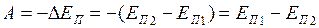. (II.82)

Работа сил гравитационного поляпри сближении двухвзаимодействующих материальных точек положительна и выражается формулой

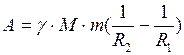, (II.83)

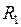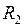где и - соответственно начальное и конечное расстояния между материальными точками ( ).

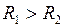Если расстояние между материальными точками увеличивается, то работа сил поля отрицательна.

Работа сил гравитационного поля при перемещении материальной точки массой из точки поля с потенциалом 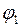в точку с потенциалом :

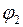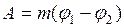. (II.84)

6. Потенциал гравитационного поля

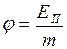, (II.85)

где 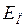- потенциальная энергия материальной точки массой , помещённой в данную точку поля.

Потенциал гравитационного поля можно выразить и через работу сил тяготения 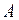, совершаемую при перемещении материальной точки массой из данной точки поля в бесконечность

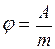. (II.86)

Работа в данном случае отрицательна.

Если поле создано материальной точкой или телом со сферически симметричным распределением плотности, то

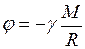, (II.87)

где 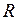- расстояние от материальной точки, создающей поле, до интересующей нас точки поля.

7. Связь между потенциалом поля тяготения и его напряжённостью

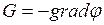. (II.88)

8. Если какое-либо тело движется в поле тяготения Земли (или другого небесного тела), то полная механическая энергия 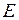тела равна сумме его кинетической и потенциальной энергии

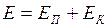(II.89)

или

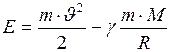, (II.90)

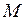где - масса тела; - масса Земли;

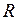- расстояние тела от центра Земли.

9. Законы Кеплера

§ Планеты движутся по эллипсам, в одном из фокусов которых находится Солнце.

§ Радиус – вектор планеты в равные времена описывают площади одинаковой величины.

§ Квадраты периодов обращения любых двух планет относятся как кубы больших полуосей их орбит

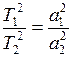. (II.91)

Законы Кеплера справедливы также для движения спутников вокруг планет.

10. Первая и вторая космические скорости

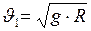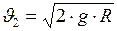; , (II.92)

где 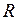- радиус Земли.

11. Основной закон динамики для неинерциальных систем отсчёта

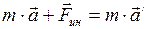, (II.93)

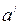где и - соответственно ускорение тела в инерциальной и неинерциальной системах отсчёта;

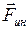- силы инерции.

12. Силы инерции

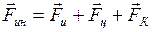, (II.94)

где 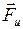- силы инерции, проявляющиеся при поступательном движении системы отсчёта с ускорением :

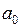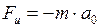; (II.95)

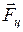- центробежные силы инерции (силы инерции, действующие во вращающейся системе отсчёта на тела, удалённые от оси вращения на конечное расстояние ):

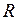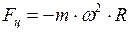. (II.96)

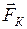- кориолисова сила инерции (силы инерции, действующие на тело, движущееся со скоростью 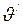во вращающейся системе отсчёта):

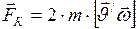. (II.97)

<35 36 373839 40 41 >

Дата добавления: 2016-09-06; просмотров: 2168;