Корреляционный анализ качественных признаков

Качественные (неколичественные) признаки (пол, образование, семейное положение, профессия, форма собственности и т.п.), взаимосвязи между ними, их влияние на другие показатели (в том числе и количественные) часто приходится изучать при проведении различных социологических исследований путем опроса или анкетирования.

[1] В вариационных рядах варианты могут быть представлены конкретными числами или интервалами, в первом случае вариационный ряд является дискретным, а во втором - интервальным.

[2] Если статистический ряд интервального типа, то в качестве вариант используют середины интервалов.

[3] Формула средней геометрической получается из средней степенной после раскрытия неопределенности при вычислении предела .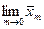

[4] Закон распределения Пуассона также называют законом редких явлений, так как он справедлив при вероятности наступления исследуемого события p≤0,1 и больших (порядка сотен единиц) объемах выборок n.

[5] Для точности расчетов будем использовать исправленное выборочное среднее квадратическое отклонение 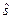, получаемое на основе исправленной выборочной дисперсии 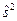. Более подробно об исправленной выборочной дисперсии см. §

[6] 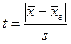; 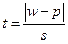- нормированное отклонение.

[7] Использование в формулах знака ≈ вместо = объясняется тем, что в практике исследований зачастую отсутствует информация о вариации признака в генеральной совокупности (в частности, о дисперсии), поэтому нередко при расчетах пользуются их приближенными значениями (оценками), вычисленными по выборке.

[8] При серийной выборке повторный отбор практически не применим, поэтому в основном используются формулы средней квадратической ошибки для бесповторного способа отбора.

[9] В практике чаще встречаются равновеликие серии, в случае неравновеликих серий необходимо использовать аналогичную взвешенную формулу (т.е. учитывать веса серий – количество единиц серий).

[10] За исключением случая, если изначально известно, что изучаемый признак Х генеральной совокупности имеет нормальное распределение N( 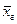,σ²), то выборочная средняя 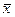при любом n (а не только при 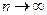) имеет нормальный закон распределения N( , ).

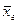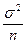[11] Значения функции распределения Стьюдента приведены в приложении 2.