Основные показатели деятельности предприятий
(данные условные)
| № предприятия | Основные производственные фонды, млн. руб. xi | Валовой выпуск продукции, млн. руб. yi | Знаки отклонений от средней величины | |
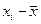
| 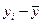
| |||
| | – | – | ||
| | – | – | ||
| | – | – | ||
| | – | – | ||
| | – | – | ||
| | + | + | ||
| | + | – | ||
| | + | + | ||
| | + | + | ||
| | + | + | ||
| Итого |
По данной таблице в целом можно сделать вывод, что чем больше стоимость основных фондов, тем больше валовой выпуск продукции, т.е. связь между рассматриваемыми факторным и результативным признаками прямая.
Такое «субъективное» суждение о наличии корреляционной связи обычно сопровождается расчетом того или иного показателя, используемого для измерения тесноты связи: коэффициента Фехнера, ранговых коэффициентов корреляции, линейного коэффициента корреляции и др.
Коэффициент Фехнера (коэффициент корреляции знаков) – простейший показатель тесноты связи, основанный на сравнении поведения отклонений индивидуальных значений факторного и результативного признаков от своей средней величины. При этом во внимание принимаются не величины отклонений ( 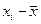 ) и (
) и ( 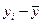 ), а их знаки («+» или «–»). Коэффициент рассчитывается по следующей формуле:
), а их знаки («+» или «–»). Коэффициент рассчитывается по следующей формуле:
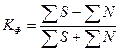 , (9.1)
, (9.1)
где 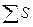 – число совпадений знаков;
– число совпадений знаков;
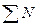 – число несовпадений знаков.
– число несовпадений знаков.
Если знаки всех отклонений по каждому признаку совпадут, то 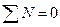 и тогда Это характеризует наличие прямой связи. Если все знаки не совпадут, то
и тогда Это характеризует наличие прямой связи. Если все знаки не совпадут, то 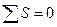 и тогда
и тогда 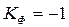 , что характеризует обратную связь. Если же
, что характеризует обратную связь. Если же  , то
, то 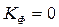 . Следовательно, коэффициент Фехнера может принимать значения от 0 до
. Следовательно, коэффициент Фехнера может принимать значения от 0 до 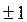 . При этом чем ближе значение к 1, тем больше (сильнее) теснота зависимости между рассматриваемыми признаками. Однако, равенство коэффициента Фехнера единице нельзя рассматривать как свидетельство функциональной связи.
. При этом чем ближе значение к 1, тем больше (сильнее) теснота зависимости между рассматриваемыми признаками. Однако, равенство коэффициента Фехнера единице нельзя рассматривать как свидетельство функциональной связи.
Для нашего примера:
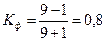
Данное значение характеризует прямую зависимость между изучаемыми признаками.
Следует иметь в виду, что поскольку коэффициент Фехнера зависит только от знаков и не учитывает величину самих отклонений X и Y от их средних величин, то он практически характеризует не столько тесноту связи, сколько ее наличие и направление.
Метод группировок
При большом числе наблюдений для выявления корреляционной связи между двумя количественными показателями X и Y удобно пользоваться методом группировок.
Чтобы выявить наличие корреляционной связи между двумя признаками, проводится группировка единиц совокупности и для каждой выделенной группы рассчитывается среднее значение результативного признака 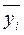 . Если результативный признак зависит от факторного признака, то в изменении среднего значения результативного признака
. Если результативный признак зависит от факторного признака, то в изменении среднего значения результативного признака  будет прослеживаться определенная закономерность.
будет прослеживаться определенная закономерность.
Таблица 9.2
Зависимость между суточной выработкой продукции (Y) и величиной основных производственных фондов (X) для совокупности 50 однотипных предприятий
| Величина ОПФ, млн. руб. (X) | Середины интервалов | Суточная выработка продукции, т (Y) | 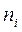
| Групповая
средняя, т,
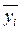
| ||||
| 7 – 11 | 11 – 15 | 15 – 19 | 19 – 23 | 23 – 27 | ||||
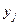
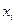
| ||||||||
| 20 – 25 | 22,5 | – | – | – | 10,3 | |||
| 25 – 30 | 27,5 | – | – | 13,3 | ||||
| 30 – 35 | 32,5 | – | – | 17,8 | ||||
| 35 – 40 | 37,5 | – | 20,3 | |||||
| 40 – 45 | 42,5 | – | – | – | 23,0 | |||
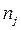
| – | |||||||
Групповая средняя, млн. руб.,
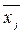
| 25,5 | 29,3 | 31,9 | 35,4 | 39,2 | – | – |

Рис. 1. График корреляционного поля и эмпирической линии регрессии
Корреляционное поле отражает не только общую зависимость между X и Y, но и концентрацию индивидуальных точек вокруг линии регрессии показателя 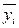 .
.
Дата добавления: 2017-05-02; просмотров: 1403;











